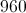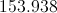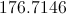All Common Core: 7th Grade Math Resources
Example Questions
Example Question #61 : Circles
The area of a circle is 

Let 
The area of a circle can be calculated as 

The circumference can be calculated as 

Example Question #4 : How To Find Circumference
The perimeter of a given rectangle is equal to the circumference of a given circle. The circle has radius 







The circumference of a circle with radius 

The perimeter of the rectangle is therefore 




Example Question #21 : Radius
A manufacturer makes wooden circles out of square blocks of wood. If the wood costs $0.25 per square inch, what is the minimum waste cost possible for cutting a circle with a radius of 44 in.?
7744 – 1936π dollars
1936 dollars
1936 – 484π dollars
5808 dollars
1936π dollars
1936 – 484π dollars
The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.) Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 88 inches for our problem. Its total area would be 88 * 88 or 7744 in2.
Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr2 or π * 442 = 1936π in2. Therefore, the area remaining would be 7744 – 1936π. The cost of the waste would be 0.25 * (7744 – 1936π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 4 from our subtraction. This would give us: 0.25 * 4 * (1936 – 484π). Since 0.25 is equal to 1/4, 0.25 * 4 = 1. Therefore, our final answer is: 1936 – 484π dollars.
Example Question #61 : Circles
A manufacturer makes wooden circles out of square blocks of wood. If the wood costs $0.20 per square inch, what is the minimum waste cost possible for cutting a circle with a radius of 25 in.?
625 - 25π dollars
625 dollars
500 - 125π dollars
500 dollars
2500 - 625π dollars
500 - 125π dollars
The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.) Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 50 inches for our problem. Its total area would be 50 * 50 or 2500 in2.
Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr2 or π * 252 = 625π in2. Therefore, the area remaining would be 2500 - 625π. The cost of the waste would be 0.2 * (2500 – 625π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 5 from our subtraction. This would give us: 0.2 * 5 * (500 – 125π). Since 0.2 is equal to 1/5, 0.2 * 625 = 125. Therefore, our final answer is: 500 – 125π dollars.
Example Question #23 : Geometry
What is the circumference of the circle provided?

In order to solve this problem, we need to recall the formula for the circumference of a circle:

The circle in this question provides us with the radius, so we can use the first formula to solve:
Solve:
Example Question #1 : Area Of A Circle
What is the area of a circle that has a diameter of 
The formula for finding the area of a circle is 


Now we use 

Example Question #1 : Know And Use The Formulas For The Area And Circumference Of A Circle: Ccss.Math.Content.7.G.B.4
What is the area of a circle with a diameter equal to 6?
First, solve for radius:
Then, solve for area:
Example Question #1 : Radius
The diameter of a circle is 
The area of a circle can be calculated using the formula:

where 


Example Question #3 : Area Of A Circle
The diameter of a circle is 

The area of a circle can be calculated using the formula:

where 


Example Question #4 : Area Of A Circle
The radius of a circle is 
The area of a circle can be calculated as 



All Common Core: 7th Grade Math Resources