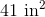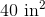All Common Core: 7th Grade Math Resources
Example Questions
Example Question #1 : Solve For Surface Area
The length of the side of a cube is . Give its surface area in terms of .
Substitute in the formula for the surface area of a cube:
Example Question #2 : Solve For Surface Area
If a cube has one side measuring cm, what is the surface area of the cube?
To find the surface area of a cube, use the formula , where represents the length of the side. Since the side of the cube measures , we can substitute in for .
Example Question #1 : Solve For Surface Area
Find the surface area of a non-cubic prism with the following measurements:
The surface area of a non-cubic prism can be determined using the equation:
Example Question #1 : How To Find The Surface Area Of A Prism
A small rectangular jewelry box has two square ends with areas of 36 square centimeters, and a width of 10 centimeters. What is the surface area of the outside of the jewelry box.
To find the surface area of the rectangular box we just need to add up the areas of all six sides. We know that two of the sides are 36 square centimeters, that means we need to find the areas of the four mising sides. To find the area of the missing sides we can just multiply the side of one of the squares (6 cm) by the width of the box:
But remember we have four of these rectangular sides:
Now we just add the two square sides and four rectangular sides to find the total surface area of the jewelry box:
That is the total surface area!
Example Question #2 : Solve For Surface Area
Alice is wrapping a rectangular box that measures . How many square feet of wrapping paper does she need?
The surface area of a rectangular prism is given by
where is the length, is the width, and is the height.
Let , , and
So the equation to solve becomes or
However the question asks for an answer in square feet. Knowing that we can convert square inches to square feet. It will take of paper to wrap the present.
Example Question #1 : Solve Problems Involving Area, Volume And Surface Area Of Two And Three Dimensional Objects: Ccss.Math.Content.7.G.B.6
Calculate the area of the provided figure.

In order to solve this problem, we need to recall the area formula for a circle:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #73 : Geometry
Calculate the area of the provided figure.

In order to solve this problem, we need to recall the area formula for a circle:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #1 : Solve For Area Of A Rectangle
Calculate the area of the provided figure.

In order to solve this problem, we need to recall the area formula for a rectangle:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #1 : Solve For Area Of A Rectangle
Calculate the area of the provided figure.

In order to solve this problem, we need to recall the area formula for a rectangle:
Now that we have the correct formula, we can substitute in our known values and solve:
Example Question #1 : Solve For Area Of A Rectangle

In rectangle ABCD, the perimeter is 48 and side BC measures 4. What is the area of rectangle ABCD?
80
48
88
72
64
80
The perimeter of a rectangle is 2L + 2W, or 2 times the length plus 2 times the width. Here you're given that side BC is 4, which means that the opposite side, AD, is also 4. So since that is two widths, you now have:
8 + 2L = 48
So 2L = 40
That means that the length is 20.
Since the area is LW, you can calculate the area as 20 * 4 = 80.
Certified Tutor
All Common Core: 7th Grade Math Resources