All Common Core: 7th Grade Math Resources
Example Questions
Example Question #1 : The Number System
Compute the following:
Convert all the double signs to a single sign before solving. Remember, two minus (negative) signs combine to form a plus (positive) sign, and a plus (positive) sign and a minus (negative) sign combine to form a minus (negative) sign.
Example Question #182 : Grade 7
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #3 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #2 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #5 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #6 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #7 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #8 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #3 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Example Question #1 : The Number System
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

All Common Core: 7th Grade Math Resources





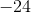










![\frac{\begin{array}[b]{r}11+x=0\\ -11\ \ \ \ -11\end{array}}{\\\\x=-11}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913177/gif.latex)






![\frac{\begin{array}[b]{r}24+x=0\\ -24\ \ \ \ -24\end{array}}{\\\\x=-24}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913198/gif.latex)






![\frac{\begin{array}[b]{r}38+x=0\\ -38\ \ \ \ -38\end{array}}{\\\\x=-38}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913145/gif.latex)






![\frac{\begin{array}[b]{r}62+x=0\\ -62\ \ \ \ -62\end{array}}{\\\\x=-62}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913221/gif.latex)






![\frac{\begin{array}[b]{r}70+x=0\\ -70\ \ \ \ -70\end{array}}{\\\\x=-70}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913224/gif.latex)






![\frac{\begin{array}[b]{r}86+x=0\\ -86\ \ \ \ -86\end{array}}{\\\\x=-86}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913120/gif.latex)






![\frac{\begin{array}[b]{r}99+x=0\\ -99\ \ \ \ -99\end{array}}{\\\\x=-99}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913562/gif.latex)






![\frac{\begin{array}[b]{r}59+x=0\\ -59\ \ \ \ -59\end{array}}{\\\\x=-59}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913234/gif.latex)






![\frac{\begin{array}[b]{r}19+x=0\\ -19\ \ \ \ -19\end{array}}{\\\\x=-19}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913482/gif.latex)



