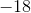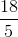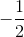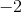All Common Core: High School - Number and Quantity Resources
Example Questions
Example Question #1 : Vector & Matrix Quantities
Vector 



In order to figure out slope, we need to remember how to find slope. Slope can be found be doing rise over run, or simply the change in 






For this example, we will let 
Below is a visual representation of what we just did. The orange arrow is 

Example Question #2 : Vector & Matrix Quantities
Vector 



In order to figure out slope, we need to remember how to find slope. Slope can be found be doing rise over run, or simply the change in 






For this example, we will let 
Below is a visual representation of what we just did. The orange arrow is 

Example Question #3 : Vector & Matrix Quantities
Vector 



In order to figure out slope, we need to remember how to find slope. Slope can be found be doing rise over run, or simply the change in 






For this example, we will let 
Below is a visual representation of what we just did. The orange arrow is 

Example Question #4 : Vector & Matrix Quantities
Vector 



In order to figure out slope, we need to remember how to find slope. Slope can be found be doing rise over run, or simply the change in 






For this example, we will let 
Below is a visual representation of what we just did. The orange arrow is 

Example Question #5 : Vector & Matrix Quantities
Vector 



In order to figure out slope, we need to remember how to find slope. Slope can be found be doing rise over run, or simply the change in 






For this example, we will let 
Below is a visual representation of what we just did. The orange arrow is 

Example Question #6 : Vector & Matrix Quantities
Vector 



In order to figure out slope, we need to remember how to find slope. Slope can be found be doing rise over run, or simply the change in 






For this example, we will let 
Below is a visual representation of what we just did. The orange arrow is 

Example Question #7 : Vector & Matrix Quantities
Vector 



In order to figure out slope, we need to remember how to find slope. Slope can be found be doing rise over run, or simply the change in 






For this example, we will let 
Below is a visual representation of what we just did. The orange arrow is 

Example Question #1 : Vector & Matrix Quantities
Vector 



In order to figure out slope, we need to remember how to find slope. Slope can be found be doing rise over run, or simply the change in 






For this example, we will let 
Below is a visual representation of what we just did. The orange arrow is 

Example Question #1 : Vector & Matrix Quantities
Vector 



In order to figure out slope, we need to remember how to find slope. Slope can be found be doing rise over run, or simply the change in 






For this example, we will let 
Below is a visual representation of what we just did. The orange arrow is 

Example Question #2 : Vector & Matrix Quantities
Vector 



In order to figure out slope, we need to remember how to find slope. Slope can be found be doing rise over run, or simply the change in 






For this example, we will let 
Below is a visual representation of what we just did. The orange arrow is 

Certified Tutor
Certified Tutor
All Common Core: High School - Number and Quantity Resources