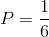All Common Core: High School - Statistics and Probability Resources
Example Questions
Example Question #1 : Understand Conditional Probability And Interpreting Independence: Ccss.Math.Content.Hss Cp.A.3
Bond A has a 10% chance of default. Bond B also has a 10% chance of default. The probability that Bond A and Bond B default is 6%.
What is the probability that Bond A defaults given that Bond B defaults? Use this result to determine if the defaults of Bond A and Bond B are independent.
60%, independent
10%, NOT independent
10%, independent
1%, independent
60%, NOT independent
60%, NOT independent
Example Question #21 : Conditional Probability & The Rules Of Probability
A group of market analysts take the inventory of a company's production of a specific sports car. The cars produced by the company vary in both color and engine size: six cylinders (i.e. V6) or eight cylinders (i.e. V8). The data is contained in the provided table.

Given that a car is jade green, what is the probability that it has a V6?
In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred. It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. Before we get into the specifics of answering this particular question, we should look at an example of conditional probability. Let's observe a dice rolling example. Suppose a person is rolling two fair dice, given that the first die equals four what is the probability that the roll's total will be less than or equal to seven. First, lets set up the equation:
Now, let's calculate the probability of rolling a four. We will do this by creating a matrix of possible outcomes. In this table, the possible values of the first die are written in the first row, while the possible values of the second die are written in the first column.

When we look at this graph, we can see that there are six possibilities of rolling a four in this scenario (they are highlighted in red in the following figure).

There are thirty-six total outcomes; therefore, the probability of rolling a four on the first die can be written as follows:
Next, we need to calculate the intersection of the probabilities of rolling a four on the first die and rolling a total less than or equal to seven. Let's start by finding out the probability of rolling a seven or less with two fair dice.

Twenty-one out of thirty-six possibilities result in a total roll value less than or equal to seven. Now, we can see where these values intersect with the probability of die one being a four.

In this table, we can see that that there are three possibilities where these two probabilities intersect; therefore, we can denote their intersection in the following manner:
Last, let's use substitution to solve our conditional probability.
Reduce.
It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
We can now use this information to answer this particular question. This question asks us to calculate the probability that a car has a V6 engine given that it is jade green in color. Let's start by constructing the conditional probability equation.
Let's use the given table to find the probability of the intersection of a car being jade green with a V6 engine.
Now, let's find the probability that a car will be jade green.
We have enough information to use substitution and solve for the conditional probability.
Simplify and solve.
Example Question #2 : Understand Conditional Probability And Interpreting Independence: Ccss.Math.Content.Hss Cp.A.3
A group of market analysts take the inventory of a company's production of a specific sports car. The cars produced by the company vary in both color and engine size: six cylinders (i.e. V6) or eight cylinders (i.e. V8). The data is contained in the provided table.
Given that a car is jade green, what is the probability that it has a V6?
In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred. It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. Before we get into the specifics of answering this particular question, we should look at an example of conditional probability. Let's observe a dice rolling example. Suppose a person is rolling two fair dice, given that the first die equals four what is the probability that the roll's total will be less than or equal to seven. First, lets set up the equation:
Now, let's calculate the probability of rolling a four. We will do this by creating a matrix of possible outcomes. In this table, the possible values of the first die are written in the first row, while the possible values of the second die are written in the first column.

When we look at this graph, we can see that there are six possibilities of rolling a four in this scenario (they are highlighted in red in the following figure).

There are thirty-six total outcomes; therefore, the probability of rolling a four on the first die can be written as follows:
Next, we need to calculate the intersection of the probabilities of rolling a four on the first die and rolling a total less than or equal to seven. Let's start by finding out the probability of rolling a seven or less with two fair dice.

Twenty-one out of thirty-six possibilities result in a total roll value less than or equal to seven. Now, we can see where these values intersect with the probability of die one being a four.

In this table, we can see that that there are three possibilities where these two probabilities intersect; therefore, we can denote their intersection in the following manner:
Last, let's use substitution to solve our conditional probability.
Reduce.
It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
We can now use this information to answer this particular question. This question asks us to calculate the probability that a car has a V6 engine given that it is jade green in color. Let's start by constructing the conditional probability equation.
Let's use the given table to find the probability of the intersection of a car being jade green with a V6 engine.
Now, let's find the probability that a car will be jade green.
We have enough information to use substitution and solve for the conditional probability.
Simplify and solve.
Example Question #3 : Understand Conditional Probability And Interpreting Independence: Ccss.Math.Content.Hss Cp.A.3
A group of market analysts take the inventory of a company's production of a specific sports car. The cars produced by the company vary in both color and engine size: six cylinders (i.e. V6) or eight cylinders (i.e. V8). The data is contained in the provided table.
Given that a car is jade green, what is the probability that it has a V6?
In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred. It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. Before we get into the specifics of answering this particular question, we should look at an example of conditional probability. Let's observe a dice rolling example. Suppose a person is rolling two fair dice, given that the first die equals four what is the probability that the roll's total will be less than or equal to seven. First, lets set up the equation:
Now, let's calculate the probability of rolling a four. We will do this by creating a matrix of possible outcomes. In this table, the possible values of the first die are written in the first row, while the possible values of the second die are written in the first column.

When we look at this graph, we can see that there are six possibilities of rolling a four in this scenario (they are highlighted in red in the following figure).

There are thirty-six total outcomes; therefore, the probability of rolling a four on the first die can be written as follows:
Next, we need to calculate the intersection of the probabilities of rolling a four on the first die and rolling a total less than or equal to seven. Let's start by finding out the probability of rolling a seven or less with two fair dice.

Twenty-one out of thirty-six possibilities result in a total roll value less than or equal to seven. Now, we can see where these values intersect with the probability of die one being a four.

In this table, we can see that that there are three possibilities where these two probabilities intersect; therefore, we can denote their intersection in the following manner:
Last, let's use substitution to solve our conditional probability.
Reduce.
It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
We can now use this information to answer this particular question. This question asks us to calculate the probability that a car has a V6 engine given that it is jade green in color. Let's start by constructing the conditional probability equation.
Let's use the given table to find the probability of the intersection of a car being jade green with a V6 engine.
Now, let's find the probability that a car will be jade green.
We have enough information to use substitution and solve for the conditional probability.
Simplify and solve.
Example Question #5 : Understand Conditional Probability And Interpreting Independence: Ccss.Math.Content.Hss Cp.A.3
A group of market analysts take the inventory of a company's production of a specific sports car. The cars produced by the company vary in both color and engine size: six cylinders (i.e. V6) or eight cylinders (i.e. V8). The data is contained in the provided table.
Given that a car is jade green, what is the probability that it has a V6?
In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred. It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. Before we get into the specifics of answering this particular question, we should look at an example of conditional probability. Let's observe a dice rolling example. Suppose a person is rolling two fair dice, given that the first die equals four what is the probability that the roll's total will be less than or equal to seven. First, lets set up the equation:
Now, let's calculate the probability of rolling a four. We will do this by creating a matrix of possible outcomes. In this table, the possible values of the first die are written in the first row, while the possible values of the second die are written in the first column.

When we look at this graph, we can see that there are six possibilities of rolling a four in this scenario (they are highlighted in red in the following figure).

There are thirty-six total outcomes; therefore, the probability of rolling a four on the first die can be written as follows:
Next, we need to calculate the intersection of the probabilities of rolling a four on the first die and rolling a total less than or equal to seven. Let's start by finding out the probability of rolling a seven or less with two fair dice.

Twenty-one out of thirty-six possibilities result in a total roll value less than or equal to seven. Now, we can see where these values intersect with the probability of die one being a four.

In this table, we can see that that there are three possibilities where these two probabilities intersect; therefore, we can denote their intersection in the following manner:
Last, let's use substitution to solve our conditional probability.
Reduce.
It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
We can now use this information to answer this particular question. This question asks us to calculate the probability that a car has a V6 engine given that it is jade green in color. Let's start by constructing the conditional probability equation.
Let's use the given table to find the probability of the intersection of a car being jade green with a V6 engine.
Now, let's find the probability that a car will be jade green.
We have enough information to use substitution and solve for the conditional probability.
Simplify and solve.
Example Question #6 : Understand Conditional Probability And Interpreting Independence: Ccss.Math.Content.Hss Cp.A.3
A group of market analysts take the inventory of a company's production of a specific sports car. The cars produced by the company vary in both color and engine size: six cylinders (i.e. V6) or eight cylinders (i.e. V8). The data is contained in the provided table.
Given that a car is jade green, what is the probability that it has a V6?
In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred. It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. Before we get into the specifics of answering this particular question, we should look at an example of conditional probability. Let's observe a dice rolling example. Suppose a person is rolling two fair dice, given that the first die equals four what is the probability that the roll's total will be less than or equal to seven. First, lets set up the equation:
Now, let's calculate the probability of rolling a four. We will do this by creating a matrix of possible outcomes. In this table, the possible values of the first die are written in the first row, while the possible values of the second die are written in the first column.

When we look at this graph, we can see that there are six possibilities of rolling a four in this scenario (they are highlighted in red in the following figure).

There are thirty-six total outcomes; therefore, the probability of rolling a four on the first die can be written as follows:
Next, we need to calculate the intersection of the probabilities of rolling a four on the first die and rolling a total less than or equal to seven. Let's start by finding out the probability of rolling a seven or less with two fair dice.

Twenty-one out of thirty-six possibilities result in a total roll value less than or equal to seven. Now, we can see where these values intersect with the probability of die one being a four.

In this table, we can see that that there are three possibilities where these two probabilities intersect; therefore, we can denote their intersection in the following manner:
Last, let's use substitution to solve our conditional probability.
Reduce.
It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
We can now use this information to answer this particular question. This question asks us to calculate the probability that a car has a V6 engine given that it is jade green in color. Let's start by constructing the conditional probability equation.
Let's use the given table to find the probability of the intersection of a car being jade green with a V6 engine.
Now, let's find the probability that a car will be jade green.
We have enough information to use substitution and solve for the conditional probability.
Simplify and solve.
Example Question #7 : Understand Conditional Probability And Interpreting Independence: Ccss.Math.Content.Hss Cp.A.3
A group of market analysts take the inventory of a company's production of a specific sports car. The cars produced by the company vary in both color and engine size: six cylinders (i.e. V6) or eight cylinders (i.e. V8). The data is contained in the provided table.
Given that a car is jade green, what is the probability that it has a V6?
In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred. It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. Before we get into the specifics of answering this particular question, we should look at an example of conditional probability. Let's observe a dice rolling example. Suppose a person is rolling two fair dice, given that the first die equals four what is the probability that the roll's total will be less than or equal to seven. First, lets set up the equation:
Now, let's calculate the probability of rolling a four. We will do this by creating a matrix of possible outcomes. In this table, the possible values of the first die are written in the first row, while the possible values of the second die are written in the first column.

When we look at this graph, we can see that there are six possibilities of rolling a four in this scenario (they are highlighted in red in the following figure).

There are thirty-six total outcomes; therefore, the probability of rolling a four on the first die can be written as follows:
Next, we need to calculate the intersection of the probabilities of rolling a four on the first die and rolling a total less than or equal to seven. Let's start by finding out the probability of rolling a seven or less with two fair dice.

Twenty-one out of thirty-six possibilities result in a total roll value less than or equal to seven. Now, we can see where these values intersect with the probability of die one being a four.

In this table, we can see that that there are three possibilities where these two probabilities intersect; therefore, we can denote their intersection in the following manner:
Last, let's use substitution to solve our conditional probability.
Reduce.
It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
We can now use this information to answer this particular question. This question asks us to calculate the probability that a car has a V6 engine given that it is jade green in color. Let's start by constructing the conditional probability equation.
Let's use the given table to find the probability of the intersection of a car being jade green with a V6 engine.
Now, let's find the probability that a car will be jade green.
We have enough information to use substitution and solve for the conditional probability.
Simplify and solve.
Example Question #8 : Understand Conditional Probability And Interpreting Independence: Ccss.Math.Content.Hss Cp.A.3
A group of market analysts take the inventory of a company's production of a specific sports car. The cars produced by the company vary in both color and engine size: six cylinders (i.e. V6) or eight cylinders (i.e. V8). The data is contained in the provided table.
Given that a car is jade green, what is the probability that it has a V6?
In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred. It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. Before we get into the specifics of answering this particular question, we should look at an example of conditional probability. Let's observe a dice rolling example. Suppose a person is rolling two fair dice, given that the first die equals four what is the probability that the roll's total will be less than or equal to seven. First, lets set up the equation:
Now, let's calculate the probability of rolling a four. We will do this by creating a matrix of possible outcomes. In this table, the possible values of the first die are written in the first row, while the possible values of the second die are written in the first column.

When we look at this graph, we can see that there are six possibilities of rolling a four in this scenario (they are highlighted in red in the following figure).

There are thirty-six total outcomes; therefore, the probability of rolling a four on the first die can be written as follows:
Next, we need to calculate the intersection of the probabilities of rolling a four on the first die and rolling a total less than or equal to seven. Let's start by finding out the probability of rolling a seven or less with two fair dice.

Twenty-one out of thirty-six possibilities result in a total roll value less than or equal to seven. Now, we can see where these values intersect with the probability of die one being a four.

In this table, we can see that that there are three possibilities where these two probabilities intersect; therefore, we can denote their intersection in the following manner:
Last, let's use substitution to solve our conditional probability.
Reduce.
It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
We can now use this information to answer this particular question. This question asks us to calculate the probability that a car has a V6 engine given that it is jade green in color. Let's start by constructing the conditional probability equation.
Let's use the given table to find the probability of the intersection of a car being jade green with a V6 engine.
Now, let's find the probability that a car will be jade green.
We have enough information to use substitution and solve for the conditional probability.
Simplify and solve.
Example Question #9 : Understand Conditional Probability And Interpreting Independence: Ccss.Math.Content.Hss Cp.A.3
A group of market analysts take the inventory of a company's production of a specific sports car. The cars produced by the company vary in both color and engine size: six cylinders (i.e. V6) or eight cylinders (i.e. V8). The data is contained in the provided table.
Given that a car is jade green, what is the probability that it has a V6?
In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred. It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. Before we get into the specifics of answering this particular question, we should look at an example of conditional probability. Let's observe a dice rolling example. Suppose a person is rolling two fair dice, given that the first die equals four what is the probability that the roll's total will be less than or equal to seven. First, lets set up the equation:
Now, let's calculate the probability of rolling a four. We will do this by creating a matrix of possible outcomes. In this table, the possible values of the first die are written in the first row, while the possible values of the second die are written in the first column.

When we look at this graph, we can see that there are six possibilities of rolling a four in this scenario (they are highlighted in red in the following figure).

There are thirty-six total outcomes; therefore, the probability of rolling a four on the first die can be written as follows:
Next, we need to calculate the intersection of the probabilities of rolling a four on the first die and rolling a total less than or equal to seven. Let's start by finding out the probability of rolling a seven or less with two fair dice.

Twenty-one out of thirty-six possibilities result in a total roll value less than or equal to seven. Now, we can see where these values intersect with the probability of die one being a four.

In this table, we can see that that there are three possibilities where these two probabilities intersect; therefore, we can denote their intersection in the following manner:
Last, let's use substitution to solve our conditional probability.
Reduce.
It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
We can now use this information to answer this particular question. This question asks us to calculate the probability that a car has a V6 engine given that it is jade green in color. Let's start by constructing the conditional probability equation.
Let's use the given table to find the probability of the intersection of a car being jade green with a V6 engine.
Now, let's find the probability that a car will be jade green.
We have enough information to use substitution and solve for the conditional probability.
Simplify and solve.
Example Question #10 : Understand Conditional Probability And Interpreting Independence: Ccss.Math.Content.Hss Cp.A.3
A group of market analysts take the inventory of a company's production of a specific sports car. The cars produced by the company vary in both color and engine size: six cylinders (i.e. V6) or eight cylinders (i.e. V8). The data is contained in the provided table.
Given that a car is jade green, what is the probability that it has a V6?
In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred. It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. Before we get into the specifics of answering this particular question, we should look at an example of conditional probability. Let's observe a dice rolling example. Suppose a person is rolling two fair dice, given that the first die equals four what is the probability that the roll's total will be less than or equal to seven. First, lets set up the equation:
Now, let's calculate the probability of rolling a four. We will do this by creating a matrix of possible outcomes. In this table, the possible values of the first die are written in the first row, while the possible values of the second die are written in the first column.

When we look at this graph, we can see that there are six possibilities of rolling a four in this scenario (they are highlighted in red in the following figure).

There are thirty-six total outcomes; therefore, the probability of rolling a four on the first die can be written as follows:
Next, we need to calculate the intersection of the probabilities of rolling a four on the first die and rolling a total less than or equal to seven. Let's start by finding out the probability of rolling a seven or less with two fair dice.

Twenty-one out of thirty-six possibilities result in a total roll value less than or equal to seven. Now, we can see where these values intersect with the probability of die one being a four.

In this table, we can see that that there are three possibilities where these two probabilities intersect; therefore, we can denote their intersection in the following manner:
Last, let's use substitution to solve our conditional probability.
Reduce.
It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
We can now use this information to answer this particular question. This question asks us to calculate the probability that a car has a V6 engine given that it is jade green in color. Let's start by constructing the conditional probability equation.
Let's use the given table to find the probability of the intersection of a car being jade green with a V6 engine.
Now, let's find the probability that a car will be jade green.
We have enough information to use substitution and solve for the conditional probability.
Simplify and solve.
Certified Tutor
Certified Tutor
All Common Core: High School - Statistics and Probability Resources