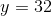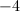GRE Math : Equations / Inequalities

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Equations / Inequalities

y = 32 $\displaystyle y = 32$

$\displaystyle y = x^2 - 4$

Quantity A: $\frac{y}{7}$ $\displaystyle \frac{y}{7}$

Quantity B: $\displaystyle x$

Possible Answers:

The two quantities are equal.

Quantity B is greater.

The relationship cannot be determined from the information given.

Quantity A is greater.

Correct answer:

The relationship cannot be determined from the information given.

Explanation:

We are given that y = 32. Plug this value of y into the second equation.

32 = x² – 4

36 = x²

x = +/– 6.

Next find a value for Quantity A:

y/7 = 32/7

This number is less than +6, but more than –6. Thus, the relationship cannot be determined from the information given.

Report an Error

Example Question #1 : Equations / Inequalities

Column A: $\left | x \right |$ $\displaystyle \left | x \right |$

Column B: x^3 $\displaystyle x^3$

Possible Answers:

The relationship cannot be determined.

Column B is greater.

Column A is greater.

The values are equal.

Correct answer:

The relationship cannot be determined.

Explanation:

Column B is greater for positive numbers.

The columns are equal for 0.

Column A is greater for negative numbers.

Because our answer changes depending on the value inserted, we cannot determine the relationship.

Report an Error

Example Question #1 : How To Find Out When An Equation Has No Solution

Find the solution to the following equation if x = 3:

y = (4x² - 2)/(9 - x²)

Possible Answers:

no possible solution

Correct answer:

no possible solution

Explanation:

Substituting 3 in for x, you will get 0 in the denominator of the fraction. It is not possible to have 0 be the denominator for a fraction so there is no possible solution to this equation.

Report an Error

Example Question #2 : Equations / Inequalities

Undefined_denom3

I. x = 0

II. x = –1

III. x = 1

Possible Answers:

II and III only

I, II, and III

II only

I only

III only

Correct answer:

I only

Explanation:

Undefined_denom2

Report an Error

Example Question #3 : Linear / Rational / Variable Equations

Nosol1

Possible Answers:

–3

There is no solution

–1/2

Correct answer:

There is no solution

Explanation:

Nosol2

Report an Error

Example Question #3 : Equations / Inequalities

$\small h\left ( x\right )=\frac{28}{x+4}$ $\displaystyle \small h\left ( x\right )=\frac{28}{x+4}$

$\small \textup{For which of the following values of}\,x\,\textup{is the above function undefined?}$ $\displaystyle \small \textup{For which of the following values of}\,x\,\textup{is the above function undefined?}$

Possible Answers:

None of the other answers

$\small 4$ $\displaystyle \small 4$

$\small -4$ $\displaystyle \small -4$

$\small 28$ $\displaystyle \small 28$

$\small 0$ $\displaystyle \small 0$

Correct answer:

$\small -4$ $\displaystyle \small -4$

Explanation:

A fraction is considered undefined when the denominator equals 0. Set the denominator equal to zero and solve for the variable.

$\small x+4=0$ $\displaystyle \small x+4=0$

$\small x=-4$ $\displaystyle \small x=-4$

Report an Error

Example Question #2 : How To Find Out When An Equation Has No Solution

Solve:

$\displaystyle 3(2x - 6) + 2x = 7x - 12$

Possible Answers:

$\displaystyle 6$

$\displaystyle -30$

$\displaystyle 10$

$\displaystyle 30$

$\displaystyle -6$

Correct answer:

$\displaystyle 6$

Explanation:

First, distribute, making sure to watch for negatives.

$\displaystyle 3(2x - 6) + 2x = 7x - 12$

$\displaystyle 6x - 18 + 2x = 7x - 12$

Combine like terms.

$\displaystyle 8x - 18 = 7x - 12$

Subtract 7x from both sides.

$\displaystyle x - 18 = -12$

Add 18 on both sides and be careful adding integers.

x = 6 $\displaystyle x = 6$

Report an Error

Example Question #5 : Linear / Rational / Variable Equations

Solve:

$\displaystyle -3(2x - 5) = 9 - 6x$

Possible Answers:

$\displaystyle 15$

$\frac{15}{9}$ $\displaystyle \frac{15}{9}$

Infinitely Many Solutions

No Solution

$\displaystyle 9$

Correct answer:

No Solution

Explanation:

First, distribute the $\displaystyle -3$ to the terms inside the parentheses.

$\displaystyle -3(2x - 5) = 9 - 6x$

$\displaystyle -6x + 15 = 9 - 6x$

Add 6x to both sides.

15 = 9 $\displaystyle 15 = 9$

This is false for any value of $\displaystyle x$. Thus, there is no solution.

Report an Error

Example Question #1 : Linear / Rational / Variable Equations

Solve $\left | 3-4x\right |<0$ $\displaystyle \left | 3-4x\right |< 0$.

Possible Answers:

No solutions

$x<\frac{3}{4}$ $\displaystyle x< \frac{3}{4}$

$x<\frac{4}{3}$ $\displaystyle x< \frac{4}{3}$

$x>\frac{3}{4}$ $\displaystyle x>\frac{3}{4}$

$x>\frac{4}{3}$ $\displaystyle x>\frac{4}{3}$

Correct answer:

No solutions

Explanation:

By definition, the absolute value of an expression can never be less than 0. Therefore, there are no solutions to the above expression.

Report an Error

Example Question #4 : Equations / Inequalities

$\displaystyle (a+b)^2 =34$

$\frac{ab}{2}=6$ $\displaystyle \frac{ab}{2}=6$

Quantity A: a^2+b^2 $\displaystyle a^2+b^2$

Quantity B: 11

Possible Answers:

Quantity B is greater

The relationship cannot be determined.

The two quantities are equal.

Quantity A is greater

Correct answer:

Quantity B is greater

Explanation:

Expand (a+b)^2 $\displaystyle (a+b)^2$ out into $\displaystyle a^2+2ab+b^2$.

Since $\frac{ab}{2}=6$ $\displaystyle \frac{ab}{2}=6$, it can be seen that 2ab=24 $\displaystyle 2ab=24$

$\displaystyle (a+b)^2 =34$

$\displaystyle a^2+b^2+24=34$

$\displaystyle a^2+b^2=10$

10<11 $\displaystyle 10< 11$ so Quantity B is greater.

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Philadelphia, MCAT Tutors in Miami, ACT Tutors in Boston, Calculus Tutors in Washington DC, French Tutors in Philadelphia, Chemistry Tutors in San Diego, Computer Science Tutors in Phoenix, Computer Science Tutors in Miami, LSAT Tutors in Miami, Physics Tutors in Philadelphia

Popular Courses & Classes

LSAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Phoenix, GMAT Courses & Classes in San Diego, SSAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Boston, SAT Courses & Classes in Miami, ACT Courses & Classes in New York City, LSAT Courses & Classes in Denver

Popular Test Prep

ISEE Test Prep in San Diego, ACT Test Prep in Dallas Fort Worth, ACT Test Prep in New York City, GMAT Test Prep in Denver, ACT Test Prep in Boston, ISEE Test Prep in Washington DC, ISEE Test Prep in San Francisco-Bay Area, GMAT Test Prep in San Diego, MCAT Test Prep in Philadelphia, MCAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Equations / Inequalities

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : Equations / Inequalities

Example Question #1 : Equations / Inequalities

Example Question #1 : How To Find Out When An Equation Has No Solution

Example Question #2 : Equations / Inequalities

Example Question #3 : Linear / Rational / Variable Equations

Example Question #3 : Equations / Inequalities

Example Question #2 : How To Find Out When An Equation Has No Solution

Example Question #5 : Linear / Rational / Variable Equations

Example Question #1 : Linear / Rational / Variable Equations

Example Question #4 : Equations / Inequalities

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details