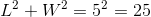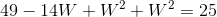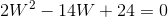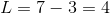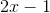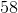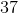GRE Math : How to find if rectangles are similar
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #1 : How To Find If Rectangles Are Similar
The perimeter of a rectangle is 14, and the diagonal connecting two vertices is 5.
Quantity A: 13
Quantity B: The area of the rectangle
Quantity B is greater.
The relationship between A and B cannot be determined.
Quantity A is greater.
The two quantities are equal.
Quantity A is greater.
One potentially helpful first step is to draw the rectangle described in the problem statement:
After that, it's a matter of using the other information given. The perimeter is given as 14, and can be written in terms of the length and width of the rectangle:
Furthermore, notice that the diagonal forms the hypotenuse of a right triangle. The Pythagorean Theorem may be applied:
This provides two equations and two unknowns. Redefining the first equation to isolate 
Plugging this into the second equation in turn gives:
Which can be reduced to:
or
Note that there are two possibile values for 
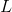
This in turn allows for the definition of the rectangle's area:
So Quantity B is 12, which is less than Quantity A.
Example Question #163 : Geometry
One rectangle has sides of 
For this problem, you need to find the pair of sides that would reduce to the same ratio as the original set of sides. This is a little tricky at first, but consider the set:
For this, you have:
Now, if you factor out 
Thus, the proportions are the same, meaning that the two rectangles would be similar.
Example Question #162 : Plane Geometry
One rectangle has a height of 
Based on the information given, we know that 
For this proportion, you really do not even need fractions. You know that 
This means that the figure would have a perimeter of
Luckily, this is one of the answers!
All GRE Math Resources
