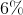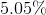GRE Math : How to find simple interest

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Interest

Harry borrowed $5000 from his parents at a rate of simple interest of 2% annually and paid it back in full in 30 months. What is the total amount of interest and principal his parents charged him?

Possible Answers:

$\$5300$

$\$5250$

none of these

$\$250$

$\$300$

Correct answer:

$\$5250$

Explanation:

Principal = $5000 (original amount)

Interest = 30 months = 2 years and a half

$\$5000 \cdot 2\%=\$100\cdot 2\ years=\$200$

half a year's interest is $1\%=\$50$

Total interest = $\$250$

Report an Error

Example Question #2 : Interest

What is the simple interest rate on an account that accrued $\$450$ after a year if the original deposit was $\$7505$ ? Round your answer to the nearest hundredth.

Possible Answers:

$16.67\%$

$6\%$

$5.05\%$

$4.56\%$

$12.41\%$

Correct answer:

$6\%$

Explanation:

The easiest way to do this is to translate the question into "is / of language." The question is asking, "What percentage of 7505 is 450 ?" Remember, is means equals and of indicates multiplication. "What" means a variable like . Therefore, we can rewrite our sentence as:

$x\cdot7505=450$

Solving for , we get:

$x=\frac{450}{7505}=0.0599600266489$

This is 5.99600266489 %. Rounding to the nearest hudredth, you get 6.00 or .

Report an Error

Example Question #1 : How To Find Simple Interest

What is the interest rate on an account if an original balance of $\$12050$ rises to $\$12670$ after one year if it is only compounded yearly?

Possible Answers:

$1.05\%$

$3.24\%$

$6.15\%$

$5.15\%$

$4.25\%$

Correct answer:

$5.15\%$

Explanation:

You can solve this by using the standard formula for simple interest (which is merely a derivative of standard applications of the formulas used for percentages in general). For our problem this is:

$(1+r)\cdot12050=12670$

Divide both sides by 12050 , but leave the fractions for the time being:

$1+r=\frac{12670}{12050}$

Solve for :

$r=\frac{12670}{12050}-1$

This is:

$r=\frac{12670-12050}{12050}=0.05145228215768$

Which is the same as:

5.145228215768 %, or 5.15 % when rounded.

Report an Error

Example Question #4 : How To Find Simple Interest

If a student borrows $200,000 at an interest rate of 6% compounded annually, when she graduates in 4 years how much money will she owe? Round to the nearest dollar.

Possible Answers:

$252,495

$257,543

$264,432

$265,432

$243,432

Correct answer:

$252,495

Explanation:

This problem requires knowledge of the compound interest formula, $A=P(1+\frac{r}{n})^{nt}$ .

Where is the amount of money owed, is the sum borrowed, is the yearly interest rate, is the amount of times the interest is compounded per year, and is the number of years. We know that the student borrowed $200,000 compounded annually at a %6 interest rate, therefore by plugging in those numbers we find that after she graduates in 4 years she will owe $252,495.

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Chicago, GMAT Tutors in Washington DC, SSAT Tutors in San Francisco-Bay Area, Statistics Tutors in Dallas Fort Worth, SAT Tutors in Philadelphia, Computer Science Tutors in Philadelphia, English Tutors in Phoenix, Physics Tutors in Seattle, Algebra Tutors in Los Angeles, Biology Tutors in Atlanta

Popular Courses & Classes

Spanish Courses & Classes in Phoenix, ACT Courses & Classes in San Diego, ACT Courses & Classes in Philadelphia, GRE Courses & Classes in Seattle, ACT Courses & Classes in Miami, GMAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Washington DC, ISEE Courses & Classes in Philadelphia, Spanish Courses & Classes in Chicago

Popular Test Prep

ACT Test Prep in San Diego, SSAT Test Prep in Houston, LSAT Test Prep in Philadelphia, SSAT Test Prep in Denver, GMAT Test Prep in Washington DC, ACT Test Prep in Philadelphia, LSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Chicago, ISEE Test Prep in Washington DC, SSAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : How to find simple interest

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : Interest

Example Question #2 : Interest

Example Question #1 : How To Find Simple Interest

Example Question #4 : How To Find Simple Interest

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details