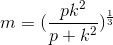All GRE Math Resources
Example Questions
Example Question #101 : Algebra
1
–2
–1
2
0
2
Example Question #1 : How To Find The Solution To A Rational Equation With Lcd
b/(m2 + 1)
–b/(m2 – 1)
bm/(m2 + 1)
–b/(m + 1)
–bm/(m2 + 1)
b/(m2 + 1)
Example Question #51 : Gre Quantitative Reasoning
In the equation below, 





Example Question #1 : How To Find The Solution To A Rational Equation With Lcd
Four less than three times a certain number is equivalent to five plus four times this same number. What is three less than three times this number?
The answer cannot be determined from the information given.
The key to solving this problem is deciphering the language and translating it into a numerical representation. The first part can be written as an equaltiy as follows:
Rearranging terms allows us to solve for this mystery number:
From there we can address the problem's question:
Example Question #52 : Gre Quantitative Reasoning
The arithmetic mean of 



Quantity A: 32
Quantity B: The arithmetic mean of 
Quantity A is greater.
Quantity B is greater.
Quantity A and Quantity B are equal.
The relationship between Quantity A and Quantity B cannot be determined.
Quantity A and Quantity B are equal.
The definition of an arithmetic mean of a set of values is given as the sum of all the values divided by the total count of values:
Where 


Quantity B can thus be defined as follows:
Which simplifies to:
or, simplifying:
We are told that the mean of 




and then as
Plugging this value into our definition of Quantity B, we can find its numerical value:
So
Example Question #5 : How To Find The Solution To A Rational Equation With Lcd
Satoshi and Reginald are bottlecap collectors, and Satoshi has 46 more bottlecaps than Reginald. If they were both to receive 6 bottle caps each, Satoshi would have three times as many bottle caps as Reginald. How many bottlecaps does Satoshi have?
The mathematical approach to this problem would be to set up a system of equations; one which represents the current relationship of Satoshi's and Reginald's number of bottle caps:
And one which represents the relationship 6 bottle caps later, wherein Satoshi would have three times as many bottlecaps as Reginald:
Subtracting the first equation from the second equation provides:
Which simplifies to
Solving this yields the value for Reginald's number of bottle caps, which is 17, which can be plugged back into the very first equation to find Satoshi's number of bottle caps, which is 63.
There is, however, another way to find this solution, which is by first looking at the answer choices.
Since we know that Satoshi's number of bottlecaps plus six must be divisible by 3 (since it is three times Reginald's new number of caps), we can quickly eliminate the choices 86, 143, and 52. Furthermore, since Satoshi has 46 more bottlecaps than Reginald, it'd be impossible for him to have 21 bottlecaps. This leaves only the 63 option.
When taking standardized math tests, where time management is key, it can be helpful to look for quicker ways to find a solution, such as back-solving, rather than just solving the problem normally.
Example Question #4 : How To Find The Solution To A Rational Equation With Lcd
Axel is traveling a distance of 120 miles to visit a relative in Phoenix. For the first half of his trip, he's traveled at a speed of 40 miles per hour. How fast will he need to drive from that point on in order to average a speed of 60 miles per hour?
To solve this problem, begin by calculating the amount of time it would take to complete the 120 mile journey at an average of 60 miles per hour:
Next, calculate the time it would take to complete half of the journey, 60 miles, at a speed of 40 miles per hour.
In order to average 60 miles per hour, the rest of the journey would need to be completed in the remaining .05 hours. Thus the speed for the final leg of the journey is determined as follows:
Well over the speed limit.
Example Question #5 : How To Find The Solution To A Rational Equation With Lcd
If 



The answer cannot be determined from the information given.
This problem has three unknowns, 


One way to begin is by solving for 
Subtracting the bottom equation from the top gives:
The next step will then be to try to combine equations in a way that will eliminate 


In order to eliminate the 
Subtracting the top from the bottom yields:
Plugging in the value for 
All GRE Math Resources