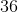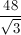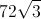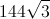All GRE Math Resources
Example Questions
Example Question #81 : Geometry
Find the perimeter of an equilateral triangle with a height of 
None of the answer choices are correct.
Perimeter is found by adding up all sides of the triangle. All sides in an equilateral triangle are equal, so we need to find the value of just one side to know the values of all sides.
The height of an equilateral triangle divides it into two equal 30:60:90 triangles, which will have side ratios of 1:2:√3. The height here is the √3 ratio, which in this case is equivalent to 8, so to get the length of the other two sides, we put 8 over √3 (8/√3) and 2 * 8/√3 = 16/√3, which is the hypotenuse of our 30:60:90 triangle.
The perimeter is then 3 * 16/√3, or 48/√3.
Example Question #2 : How To Find The Perimeter Of An Equilateral Triangle
If the height of an equilateral triangle is 
By having a height in an equilateral triangle, the angle is bisected therefore creating two 
The height is opposite the angle 
Side opposite 








Since each side is the same and there are three sides, we just multply the answer by three to get 
Example Question #3 : How To Find The Perimeter Of An Equilateral Triangle
If area of equilateral triangle is 
The area of an equilateral triangle is 
So let's set-up an equation to solve for 


The 

Then take square root on both sides and we get 


Example Question #82 : Geometry
What is the length of a side of an equilateral triangle if the area is 
The area of an equilateral triangle is 
So let's set-up an equation to solve for 


The 

Then take square root on both sides and we get 
Example Question #83 : Geometry
If the height of the equilateral triangle is 
By having a height in an equilateral triangle, the angle is bisected therefore creating two 
The height is opposite the angle 
Side opposite 







Example Question #2 : Equilateral Triangles
What is the area of an equilateral triangle with a base of 
An equilateral triangle can be considered to be 2 identical 30-60-90 triangles, giving the triangle a height of 
Example Question #3 : Equilateral Triangles

An equilateral triangle is inscribed into a circle of radius 10. What is the area of the triangle?
The answer cannot be determined from the information given.
To solve this equation, first note that a line drawn from the origin to a vertex of the equilateral triangle will bisect the angle of the vertex. Furthermore, the length of this line is equal to the radius:

That this creates in turn is a 30-60-90 right triangle. Recall that the ratio of the sides of a 30-60-90 triangle is given as:
Therefore, the length of the 
This is also one half of the base of the triangle, so the base of the triangle can be found to be:
Furthermore, the length of the 
The vertical section rising from the origin is the length of the radius, which when combined with the shorter section above gives the height of the triangle:
The area of a triangle is given by one half the base times the height, so we can find the answer as follows:
Example Question #1 : How To Find The Area Of An Equilateral Triangle
Find the area of an equilateral triangle when one of its sides equals 4.
4√3
4
8
2√3
4√3
All sides of an equilateral triangle are equal, so all sides of this triangle equal 4.
Area = 1/2 base * height, so we need to calculate the height: this is easy for an equilateral triangle, since you can bisect any such triangle into two identical 30:60:90 triangles.
The ratio of lengths of a 30:60:90 triangle is 1:√3:2. The side of the equilateral triangle is 4, and we divided the base in half when we bisected the triangle, so that give us a length of 2, so our triangle must have sides of 2, 4, and 2√3; thus we have our height.
One of our 30:60:90 triangles will have a base of 2 and a height of 2√3. Half the base is 1, so 1 * 2√3 = 2√3.
We have two of these triangles, since we divided the original triangle, so the total area is 2 * 2√3 = 4√3.
You can also solve for the area of any equilateral triangle by applying the formula (s2√3)/4, where s = the length of any side.
Example Question #1 : How To Find The Height Of An Equilateral Triangle
One side of an equilateral triangle is equal to
Quantity A: The area of the triangle.
Quantity B:
Quantity B is greater.
The two quantities are equal.
Quantity A is greater.
The relationship cannot be determined.
Quantity B is greater.
To find the area of an equilateral triangle, notice that it can be divided into two 

The ratio of sides in a 





The formula for the area of the triangle is given as:
So the area of an equilateral triangle can be written in term of the lengths of its sides as:
For this particular triangle, since 

If the relation between ratios is hard to visualize, realize that
Example Question #4 : Equilateral Triangles
If the area of an equilateral triangle is 
The area of an equilateral triangle is 
So let's set-up an equation to solve for 


The 

Then take square root on both sides and we get 


The height is opposite the angle 







We can simplify this by factoring out a 

All GRE Math Resources