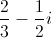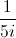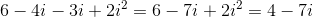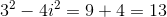All GRE Subject Test: Math Resources
Example Questions
Example Question #1 : Sat Subject Test In Math I
Evaluate
You cannot divide by complex numbers
To divide by a complex number, we must transform the expression by multiplying it by the complex conjugate of the denominator over itself. In the problem, 


We can then combine like terms and rewrite all 

Our final answer is therefore
Example Question #1 : Complex Conjugates
Simplify:
To get rid of the fraction, multiply the numerator and denominator by the conjugate of the denominator.
Now, multiply and simplify.
Remember that
Example Question #41 : Imaginary Numbers & Complex Functions
Simplify:
To get rid of the fraction, multiply the numerator and denominator by the conjugate of the denominator.
Now, multiply and simplify.
Remember that
Example Question #31 : Number Lines And Absolute Value
Divide:
The answer must be in standard form.
Multiply both the numerator and the denominator by the conjugate of the denominator which is 
The numerator after simplification give us
The denominator is equal to
Hence, the final answer in standard form =
Example Question #41 : Imaginary Numbers & Complex Functions
The definition of a complex conjugate is each of two complex numbers with the same real part and complex portions of opposite sign.
Example Question #42 : Imaginary Numbers & Complex Functions
Which of the following is the complex conjugate of 
The complex conjugate of a complex equation 

The complex conjugate when multiplied by the original expression will also give me a real answer.
The complex conjugate of 
Example Question #43 : Imaginary Numbers & Complex Functions
Simplify
In problems like this, you are expected to simplify by removing i from the denominator. To do this, multiply the numerator and denominator by the conjugate of the denominator (switch the sign between the two terms from either a plus to a minus or vice versa) over itself. The conjugate over itself equals 1 and does not change the value of the expression (any number multiplied by 1 is still that number). Multiplying by the conjugate is the only way to eliminate i since there will be no middle term when we foil.
Simplify i squared to -1 and then combine like terms
Example Question #1 : Complex Conjugates
Simplify
In problems like this, you are expected to simplify by removing i from the denominator. To do this, multiply the numerator and denominator by the conjugate of the denominator (switch the sign between the two terms from either a plus to a minus or vice versa) over itself. The conjugate over itself equals 1 and does not change the value of the expression (any number multiplied by 1 is still that number). Multiplying by the conjugate is the only way to eliminate i since there will be no middle term when we foil.
Simplify i squared to be -1 and then combine like terms
Example Question #45 : Imaginary Numbers & Complex Functions
Simplify
In problems like this, you are expected to simplify by removing i from the denominator. To do this, multiply the numerator and denominator by the conjugate of the denominator (switch the sign between the two terms from either a plus to a minus or vice versa) over itself. The conjugate over itself equals 1 and does not change the value of the expression (any number multiplied by 1 is still that number). Multiplying by the conjugate is the only way to eliminate i since there will be no middle term when we foil.
Simplify i squared to be -1 and then combine like terms
Example Question #1 : Complex Conjugates
Simplify
In problems like this, you are expected to simplify by removing i from the denominator. To do this, multiply the numerator and denominator by the conjugate of the denominator (switch the sign between the two terms from either a plus to a minus or vice versa) over itself. The conjugate over itself equals 1 and does not change the value of the expression (any number multiplied by 1 is still that number). Multiplying by the conjugate is the only way to eliminate i since there will be no middle term when we foil.
Simplify i squared to be -1 and then combine like terms
The coefficients of all the terms can divide by 4 so reduce each of them
All GRE Subject Test: Math Resources