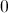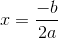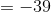All High School Math Resources
Example Questions
Example Question #3 : Pre Calculus
What is the minimal value of
over all real numbers?
Possible Answers:
No minimum value.
Correct answer:
Explanation:
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The 
is at
So here,
We plug this value back into the equation of the parabola, to find the value of the function at this 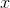
Thus the minimal value of the expression is 
All High School Math Resources
Popular Subjects
Calculus Tutors in Boston, Reading Tutors in Boston, Physics Tutors in Phoenix, French Tutors in Denver, Calculus Tutors in Phoenix, GMAT Tutors in Seattle, Reading Tutors in Chicago, Biology Tutors in Washington DC, Algebra Tutors in Philadelphia, SSAT Tutors in Chicago
Popular Courses & Classes
LSAT Courses & Classes in Denver, GMAT Courses & Classes in San Diego, GRE Courses & Classes in Miami, GRE Courses & Classes in Houston, GMAT Courses & Classes in New York City, ACT Courses & Classes in Denver, LSAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Philadelphia, SAT Courses & Classes in Miami
Popular Test Prep
GMAT Test Prep in New York City, GRE Test Prep in Dallas Fort Worth, ISEE Test Prep in Houston, MCAT Test Prep in Phoenix, LSAT Test Prep in San Diego, MCAT Test Prep in Seattle, MCAT Test Prep in Los Angeles, MCAT Test Prep in Boston, SAT Test Prep in New York City, GRE Test Prep in Los Angeles