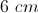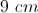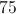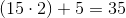$\displaystyle A=\frac{1}{2}bh$. 

$\displaystyle 6x=42$

$\displaystyle x=7$

Because this is an acute isosceles triangle, the third side must be the same as the longer of the sides that you were given.  To find the perimeter, multiply the longer side by 2 and add the shorter side.

$\displaystyle (15\cdot2)+5=35$

A triangle has 180 degrees.  An isoceles triangle has one vertex angle and two congruent base angles.

Let $\displaystyle x$ = vertex angle and $\displaystyle 2x+5$ =  base angle

So the equation to solve becomes

$\displaystyle x+2x+5+2x+5 = 180$ or $\displaystyle 5x+10=180$

So the vertex angle is $\displaystyle 34^{\circ}$ and the base angle is $\displaystyle 73^{\circ}$ so the difference is $\displaystyle 39^{\circ}$

Because line segments ZA and ZB are radii of the circle, they must have the same length. That makes triangle ABZ an isosceles triangle, with <ZAB and <ZBA having the same measure. Because the three angles of a triangle must sum to 180°, you can express this in the equation:

140 + 2x = 180 --> 2x = 40 --> x = 20

It's good to draw a diagram for this; we know that it's an isosceles triangle; remember that the angles of a triangle total 180 degrees.

Angle G for this triangle is the one angle that doesn't correspond to an equal side of the isosceles triangle (opposite side to the angle), so that means ∠F = ∠H, and that ∠F + ∠H + 40 = 180,

By substitution we find that ∠F * 2 = 140 and angle F = 70 degrees. 

An isosceles triangle has two congruent base angles and one vertex angle.  Each triangle contains $\displaystyle 180^{\circ}$.  Let $\displaystyle x$ = base angle, so the equation becomes $\displaystyle 54 + x + x = 180$.  Solving for $\displaystyle x$ gives $\displaystyle x = 63$

Every triangle has 180 degrees.  An isosceles triangle has one vertex angle and two congruent base angles.

Let $\displaystyle x$ = the vertex angle

and $\displaystyle 2x - 5$ = base angle

So the equation to solve becomes 

$\displaystyle x + (2x - 5) + (2x - 5) = 180$

or

$\displaystyle 5x - 10 = 180$

Thus the vertex angle is 38 and the base angle is 71 and their sum is 109.

This triangle has an angle of $\displaystyle 65^{\circ}$. We also know it has another angle of $\displaystyle 65^{\circ}$ at $\displaystyle \angle ABC$ because the two sides are equal. Adding those two angles together gives us $\displaystyle 130^{\circ}$ total. Since a triangle has $\displaystyle 180^{\circ}$ total, we subtract 130 from 180 and get 50.

All triangles contain $\displaystyle 180$ degrees.  An isosceles triangle has one vertex angle and two congruent base angles.

Let $\displaystyle x = base$ and $\displaystyle 2x+20 = vertex$.

So the equation to solve becomes $\displaystyle 2x+20+x+x=180$.

We get $\displaystyle x=40$ and $\displaystyle 2x+20 = 100$, so the sum of the base and vertex angles is $\displaystyle 140$.

In order for a triangle to be an isosceles triangle, it must contain two equivalent angles and one angle that is different. Given that one angle is greater than 100 degrees: $\displaystyle 180 - 100 = 80 \: degrees.$ Thus, the sum of the other two angles must be less than 80 degrees. If an angle is represented by $\displaystyle z$: $\displaystyle 2z < 80\: degrees = z < 40\: degrees.$