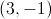All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find The Midpoint Of A Line Segment
What is the midpoint between 

The midpoint is given by taking the mean, or average, of the 

Let 
So the midpoint formula becomes 
So the midpoint is
Example Question #1 : Midpoint Formula
What is the midpoint of a line segment connecting the points 
Use the midpoint formula:
Example Question #1 : Midpoint Formula
Given two points 

What is the midpoint of the line segment? Addtionally, what is the length of the line segment?
Midpoint:
Length:
Midpoint:
Length:
Midpoint:
Length:
Midpoint:
Length:
Midpoint:
Length:
Midpoint:
Length:
The midpoint formula is as follows:
This makes sense; it is as simple as the average of the 

For this problem, 
So the midpoint is
The distance formula is as follows:
The order you put the first and second components of each point does NOT matter, when a positive or negative number is squared, it will always come out positive.
So the distance is
Example Question #2 : Coordinate Geometry
Find the midpoint of a line segment going from 

To find the midpoint of a line segment, you must find the mean of the x values and the mean of the y values.
Our x values are 


Our y values are 



Example Question #2 : How To Find The Midpoint Of A Line Segment
Find the coordinate of the midpoint of the line segment connecting the pair of points


Cannot be determined
The coordinate of the midpoint of the line segment connecting a pair of points is
So for the pair of points 

we get:
Example Question #1 : Coordinate Geometry
Find the coordinate of the midpoint of the line segment connecting the pair of points


Cannot be determined
The coordinate of the midpoint of the line segment connecting a pair of points is

So for the pair of points 
we get,
Example Question #2 : Midpoint Formula
A line extends from the origin to 
The origin is the point 






Note that since the first point is the origin, we're averaging these points with 0, or in other words just dividing by 2.
Example Question #8 : Midpoint Formula
There is a line segment between the two points (5, 10) and (3, 6). What formula will give you the correct mid-point of the line segment?
To find the mid-point given two points on the coordinate plane you are basically finding the average of the x-values and the average of the y-values. To do this follow the formula below:
With our points this gives:
Example Question #1 : Midpoint Formula
A line has endpoints at (4,5) and (-6,8). Where is its midpoint?
The midpoint is the point that is equidistant from each endpoint point.
We find it using a formula that computes the average of the x and y coordinates.
Example Question #1291 : Intermediate Geometry
A line segment has the endpoints 

Recall the formula for finding a midpoint of a line segment:
The coordinates of the midpoint is just the average of the x-coordinates and the average of the y-coordinates.
Plug in the given points to find the midpoint of the line segment.
All Intermediate Geometry Resources