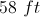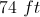Intermediate Geometry : How to find the perimeter of a trapezoid
Study concepts, example questions & explanations for Intermediate Geometry
All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of A Trapezoid
Find the perimeter of the following trapezoid.
The answer is 50 ft. In order to find the perimeter, you must find the length of the left side. After some deduction 
Once you find that the last side is 8 ft, you can add
to get an answer of 50 ft. for the perimeter.
Example Question #2 : How To Find The Perimeter Of A Trapezoid
The height of a trapezoid is 
Find the perimeter of the trapezoid to the nearest hundreth.
Use the triangle formed by the height of the trapezoid to find the lengths of the two sides of the trapezoid and the length of 
This finds the base of the triangle, which can be added twice to 
Now, use the same triangle to find the length of the sides.
Lastly, add all of the lengths together: 
Example Question #1 : How To Find The Perimeter Of A Trapezoid
Find the perimeter of the trapezoid below.
We can then use the Pythagorean Theorem to find the right portion of the bottom base. We can then use this value to determine the left portion.
Using Pythagorean Theorem again, we can calculate the left leg to be 20. That means we now know all four sides. The perimeter is simply the sum.
Example Question #1 : How To Find The Perimeter Of A Trapezoid
An isosceles trapezoid has two bases that are parallel to each other. The larger base is 
What is the perimeter of the trapezoid?
To find the perimeter of this trapezoid, first find the length of the larger base. Then, find the sum of all of the sides. It's important to note that since this is an isosceles trapezoid, both of the non-parallel sides will have the same length.
The solution is:
The smaller base is equal to 
Example Question #1 : How To Find The Perimeter Of A Trapezoid
Dr. Robinson's property is shaped like an isosceles trapezoid. Dr. Robinson gave a contractor the following measurements, so that the contractor can build a wall around the enire property.
Measurements of property:
Find the perimeter of Dr. Robinson's property.
The measurements that Dr. Robinson gave to the contractor include the lengths of the two base sides and one of the non-parallel sides of the property. Since Dr. Robinson's property is shaped like an isosceles trapezoid, there must be two non-parallel sides of equal length.
The solution is:
Certified Tutor
All Intermediate Geometry Resources
