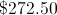Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Middle Level Quantitative : Whole and Part

Study concepts, example questions & explanations for ISEE Middle Level Quantitative

Create An Account

All ISEE Middle Level Quantitative Resources

6 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Part From The Whole

Harvey bought a suit at a 25% employee discount at the store where he works. The suit originally cost $350.00. How much did he end up paying?

Possible Answers:

$\$300.00$

$\$ 262.50$

$\$272.50$

$\$280.00$

$\$250.00$

Correct answer:

$\$ 262.50$

Explanation:

Finding 25% of a number is the same as multiplying it by 0.25; to get the discount, multiply 0.25 by the original purchase price of $350.00

$0.25 \cdot \$350 = \$87.50$

To get the price Harvey paid, subtract the discount from the original price:

$\$350 - \$87.50 = \$ 262.50$

Report an Error

Example Question #872 : Isee Middle Level (Grades 7 8) Quantitative Reasoning

$A + B \equiv 5 \textrm{ mod } 9$

Which of the following is true if A = 8 ?

Possible Answers:

B = 4

B = 6

B = 8

B = 2

Correct answer:

B = 6

Explanation:

Two expressions are equivalent in modulo 9 arithmetic if and only if, when each is divided by 9, the same remainder is yielded.

$A + B \equiv 5 \textrm{ mod } 9$ ,

$8 + B \equiv 5$

$8 + B - 8 \equiv 5 - 8$

$B \equiv 5 - 8$

$B \equiv -3$

B = -3 + 9 = 9-3 = 6 , so

B = 6 is the correct choice.

Report an Error

Example Question #2 : How To Find The Part From The Whole

is a positive integer. Which is the greater quantity?

(a) The remainder if is divided by 5

(b) The remainder if is divided by 4

Possible Answers:

(b) is the greater quantity

It is impossible to determine which is greater from the information given

(a) and (b) are equal

(a) is the greater quantity

Correct answer:

It is impossible to determine which is greater from the information given

Explanation:

The information is insufficient.

For example, if X = 10 :

$4X = 4 \cdot 10 = 40$ .

$40 \div 5 = 8 \textrm{ R }0$

$5X = 5 \cdot 10 = 50$ .

$50 \div 4 = 12\textrm{ R }2$

This gives the division in (b) the greater remainder.

But if X= 12 :

$4X = 4 \cdot 12 = 48$ .

$48 \div 5 = 9 \textrm{ R }3$

$5X = 5 \cdot 12 = 60$ .

$60 \div 4 = 15\textrm{ R }0$

This gives the division in (a) the greater remainder.

Report an Error

Example Question #1 : Whole And Part

is a positive even integer. Which is the greater quantity?

(a) The remainder if 3 X is divided by 6

(b) The remainder if is divided by 3.

Possible Answers:

(a) is the greater quantity

(b) is the greater quantity

It is impossible to determine which is greater from the information given

(a) and (b) are equal

Correct answer:

(a) and (b) are equal

Explanation:

Since is an even integer, by definition, there is an integer such that

X = 2Y .

$3 X = 3 \cdot 2Y = 6Y$ ; therefore,

$3X \div 6 = 6Y \div 6 = Y$ ; the remainder is 0.

Also,

$6X \div 3 =2X$ ; the remainder is 0.

The two remainders are both equal to 0.

Report an Error

Example Question #2 : How To Find The Part From The Whole

is a positive odd integer. Which is the greater quantity?

(a) The remainder if is divided by 8

(b) The remainder if is divided by 4

Possible Answers:

(a) is the greater quantity

(b) is the greater quantity

(a) and (b) are equal

It is impossible to determine which is greater from the information given

Correct answer:

(a) is the greater quantity

Explanation:

$8X \div 4 = 2X$ , with a remainder of 0.

If $4X \div 8$ were to yield a remainder of 0, then $4X \div 8 = \frac{1}{2} X$ must be a whole number; this can only happen if is even. Since is odd, it follows that $\frac{1}{2} X$ is not a whole number, and $4X \div 8$ must yield a nonzero remainder. (a) must be the greater quantity.

Report an Error

Example Question #1 : Whole And Part

150% of what number is 9,000?

Possible Answers:

6,300

5,000

6,000

7,200

7,500

Correct answer:

6,000

Explanation:

Taking 150% of a number is the same as multiplying that number by 1.5. We can find our number, therefore, by dividing 9,000 by 1.5:

$9,000 \div 1.5 = 6,000$

Report an Error

Example Question #2 : Whole And Part

is a multiple of 2, but not a multiple of 6. If is divided by 6, What could be the remainder?

Possible Answers:

Correct answer:

Explanation:

If the remainder of dividing by 6 is 0, then must be a multiple of 6, which contradicts what we are given.

Suppose we call and the quotient and remainder, respectively, of dividing by 6. Then

$6 \cdot Q + R = X$

If the remainder is 1, then

$6 \cdot Q + 1 = X$

$6 \cdot Q$ , as a product of two integers, one even, is an even number; if 1 is added, the result is odd. Therefore, if 1 is the remainder, is odd, which also contradicts what we are given about . 1 cannot be the remainder, and for similar reasons, neither can 3.

This leaves 2, which can be the remainder; for example, 8, which is a multiple of 2, but not a multiple of 6, yields a quotient of 1 and a remainder of 2 when divided by 2.

Report an Error

View Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View Tutors

Yongmao
Certified Tutor

Nankai University, Bachelor of Science, Chemistry. Washington University in St Louis, Doctor of Philosophy, Organic Chemistry.

View Tutors

Linda
Certified Tutor

Long Island University-C W Post Campus, Bachelors, Art Education.

All ISEE Middle Level Quantitative Resources

6 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Chicago, SSAT Tutors in Atlanta, Algebra Tutors in Chicago, Algebra Tutors in Miami, Biology Tutors in Phoenix, Chemistry Tutors in Phoenix, English Tutors in San Francisco-Bay Area, Statistics Tutors in Seattle, GMAT Tutors in Denver, Reading Tutors in New York City

Popular Courses & Classes

SSAT Courses & Classes in Philadelphia, SAT Courses & Classes in Philadelphia, SAT Courses & Classes in San Diego, LSAT Courses & Classes in Boston, GRE Courses & Classes in Denver, Spanish Courses & Classes in San Diego, GRE Courses & Classes in Seattle, Spanish Courses & Classes in Boston, Spanish Courses & Classes in Atlanta, ISEE Courses & Classes in San Diego

Popular Test Prep

SSAT Test Prep in Washington DC, SAT Test Prep in Miami, ISEE Test Prep in Chicago, GRE Test Prep in Denver, ACT Test Prep in Boston, GMAT Test Prep in New York City, MCAT Test Prep in San Diego, MCAT Test Prep in Los Angeles, ISEE Test Prep in Philadelphia, GRE Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Middle Level Quantitative : Whole and Part

Study concepts, example questions & explanations for ISEE Middle Level Quantitative

All ISEE Middle Level Quantitative Resources

Example Questions

Example Question #1 : How To Find The Part From The Whole

Example Question #872 : Isee Middle Level (Grades 7 8) Quantitative Reasoning

Example Question #2 : How To Find The Part From The Whole

Example Question #1 : Whole And Part

Example Question #2 : How To Find The Part From The Whole

Example Question #1 : Whole And Part

Example Question #2 : Whole And Part

All ISEE Middle Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: