Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : How to use a Venn Diagram

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Venn Diagrams

Venn

Refer to the above Venn diagram.

Define universal set $U = \mathbb{N}$ , the set of natural numbers.

Define sets and as follows:

$A = \left \{ 1,5,9,13,17,21,... \right \}$

$B = \left \{ 2,5,8,11,14,17...\right \}$

Which of the following numbers is an element of the set represented by the gray area in the diagram?

Possible Answers:

105

103

102

104

101

Correct answer:

104

Explanation:

The gray area represents the set of all elements that are in but not in .

is the set of integers that, when divided by 3, yield remainder 2. Therefore, we can eliminate 102 and 105, both multiples of 3, and 103, which, when divided by 3, yields remainder 1.

is the set of integers that, when divided by 4, yield remainder 1. Since we do not want an element from this set, we can eliminate 101, but not 104.

104 is the correct choice.

Report an Error

Example Question #2 : Venn Diagrams

Venn

In the above Venn diagram, the universal set is defined as $U = \left \{ a, b, c, d, e, f, g, h\right \}$ . Each of the eight letters is placed in its correct region.

What is $A \cap B$ ?

Possible Answers:

$A \cap B = \left \{ a,b,d,e,f,g,h \right \}$

$A \cap B = \left \{ b,d,e,g,h \right \}$

$A \cap B = \left \{ a,f \right \}$

$A \cap B = \left \{ a,c,f \right \}$

$A \cap B = \left \{ b,c,d,e,g,h \right \}$

Correct answer:

$A \cap B = \left \{ a,f \right \}$

Explanation:

$A \cap B$ is the intersection of sets and - that is, the set of all elements of that are elements of both and . We want all of the letters that fall in both circles, which from the diagram can be seen to be and . Therefore,

$A \cap B = \left \{ a,f \right \}$

Report an Error

Example Question #3 : Data Analysis And Probability

Venn

In the above Venn diagram, the universal set is defined as $U = \left \{ a, b, c, d, e, f, g, h\right \}$ . Each of the eight letters is placed in its correct region. Which of the following is equal to $\overline{A\cap B}$ ?

Possible Answers:

$\overline{A\cap B} = \left \{ b,d,e,g,h\right \}$

$\overline{A\cap B} = \left \{ c\right \}$

$\overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}$

$\overline{A\cap B} = \left \{ a,f\right \}$

$\overline{A\cap B} = \left \{ a,c,f\right \}$

Correct answer:

$\overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}$

Explanation:

$\overline{A \cap B}$ is the complement of $A \cap B$ - the set of all elements in not in $A \cap B$ .

$A \cap B$ is the intersection of sets and - that is, the set of all elements of that are elements of both and . Therefore, $\overline{A \cap B}$ is the set of all elements that are not in both and , which can be seen from the diagram to be all elements except and . Therefore,

$\overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}$ .

Report an Error

Example Question #4 : Data Analysis And Probability

Venn

Possible Answers:

$\overline{A\cup B} = \left \{ b,d,e,g,h\right \}$

$\overline{A\cup B} = \left \{ a,c,f\right \}$

$\overline{A\cup B} = \left \{ c\right \}$

$\overline{A\cup B} = \left \{ b,c,d,e,g,h\right \}$

$\overline{A\cup B} = \left \{ a,f\right \}$

Correct answer:

$\overline{A\cup B} = \left \{ c\right \}$

Explanation:

$\overline{A\cup B}$ is the complement of $A\cup B$ - the set of all elements in not in $A\cup B$ .

$A\cup B$ is the union of sets and - the set of all elements in either or . Therefore, $\overline{A\cup B}$ is the set of all elements in neither nor , which can be seen from the diagram to be only one element - . Therefore,

$\overline{A\cup B} = \left \{ c\right \}$

Report an Error

Example Question #1 : How To Use A Venn Diagram

The following Venn diagram depicts the number of students who play hockey, football, and baseball. How many students play football and baseball?

Problem_9

Possible Answers:

Correct answer:

Explanation:

The number of students who play football or baseball can by finding the summer of the number of students who play football alone, baseball alone, baseball and football, and all three sports.

30+20+3+3=56

Report an Error

Example Question #2 : Data Analysis And Probability

A class of students was asked whether they have cats, dogs, or both.The results are depicted in the following Venn diagram. How many students do not have a dog?

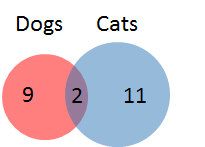
Question_5

Possible Answers:

Correct answer:

Explanation:

First, calculate the number of students with a dog:
9+2=11

Next, subtract the number of students with a dog from the total number of students.

30-11=19

Report an Error

View Tutors

Myung Hee
Certified Tutor

Pukyung National University, Bachelor of Science, Japanese Studies. University of Padova, Master of Science, International Bu...

View Tutors

Dehlly
Certified Tutor

Universidad Nacional de Colombia, Bachelor in Business Administration, Mathematics and Statistics. Columbia University in th...

View Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Miami, SAT Tutors in Chicago, Math Tutors in Atlanta, Calculus Tutors in Denver, Biology Tutors in Chicago, Algebra Tutors in Los Angeles, MCAT Tutors in Philadelphia, SSAT Tutors in Phoenix, MCAT Tutors in San Francisco-Bay Area, Algebra Tutors in Chicago

Popular Courses & Classes

ACT Courses & Classes in Atlanta, SSAT Courses & Classes in Washington DC, GRE Courses & Classes in Denver, MCAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Houston, GMAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Atlanta, SAT Courses & Classes in Philadelphia, Spanish Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Dallas Fort Worth

Popular Test Prep

GRE Test Prep in Seattle, GMAT Test Prep in Los Angeles, ISEE Test Prep in Denver, ACT Test Prep in San Diego, ACT Test Prep in Atlanta, ISEE Test Prep in New York City, MCAT Test Prep in Chicago, SSAT Test Prep in Phoenix, SSAT Test Prep in Atlanta, LSAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : How to use a Venn Diagram

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #1 : Venn Diagrams

Example Question #2 : Venn Diagrams

Example Question #3 : Data Analysis And Probability

Example Question #4 : Data Analysis And Probability

Example Question #1 : How To Use A Venn Diagram

Example Question #2 : Data Analysis And Probability

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: