Call Now to Set Up Tutoring:

(888) 888-0446

MAP 7th Grade Math : Geometry

Study concepts, example questions & explanations for MAP 7th Grade Math

Create An Account

All MAP 7th Grade Math Resources

5 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

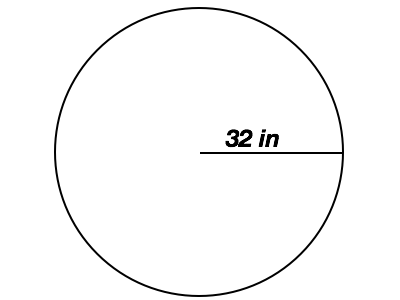
Example Question #1 : Geometry

What is the area of the circle provided?

Possible Answers:

$1\textup,023\pi\textup{ in}^2$

$1\textup,026\pi\textup{ in}^2$

$1\textup,025\pi\textup{ in}^2$

$1\textup,024\pi\textup{ in}^2$

Correct answer:

$1\textup,024\pi\textup{ in}^2$

Explanation:

In order to solve this problem, we need to recall the formula for the area of a circle:

$A= r^2\pi$

The circle in this question provides us with the radius, so we can use the formula to solve:

$A=32^2\pi$

Solve:

$A=1\textup,024\pi\textup{ in}^2$

Report an Error

Example Question #2 : Geometry

The figure represents a set of complementary angles, solve for .

Possible Answers:

$71^\circ$

$68^\circ$

$70^\circ$

$69^\circ$

Correct answer:

$70^\circ$

Explanation:

Complementary angles are defined as two angles that when added together equal $90^\circ$

From the question, we know that the two angles are complimentary, and thus equal $90^\circ$ , so we can set up the following equation:

x+20=90

Next we can solve for :

$\frac{\begin{array}[b]{r}x+20=90\\ -20-20\end{array}}{x= 70}$

Report an Error

Example Question #3 : Geometry

Calculate the volume of the provided figure.

Possible Answers:

$213\textup{ in}^3$

$215\textup{ in}^3$

$216\textup{ in}^3$

$214\textup{ in}^3$

Correct answer:

$216\textup{ in}^3$

Explanation:

In order to solve this problem, we need to recall the volume formula for a cube:

$V=l\times w\times h$

Now that we have the correct formula, we can substitute in our known values and solve:

$V=6\times6\times6$

$V=216\textup{ in}^3$

Report an Error

View Tutors

Anjali
Certified Tutor

Delhi University, Bachelor of Science, Physics. Kumuan University, Master of Science, Physics.

View Tutors

Pankaj
Certified Tutor

University of Delhi, Electrical Engineer, Electrical Engineering. Columbia University in the City of New York, Master of Arts...

View Tutors

Bhavana
Certified Tutor

Indian Institute of Science Education and Research, Tirupati, Master's/Graduate, Physics and biology .

All MAP 7th Grade Math Resources

5 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Phoenix, Algebra Tutors in Philadelphia, Reading Tutors in Washington DC, GRE Tutors in Houston, GMAT Tutors in Philadelphia, Math Tutors in Boston, Reading Tutors in San Francisco-Bay Area, Statistics Tutors in Philadelphia, Computer Science Tutors in Houston, Reading Tutors in Chicago

Popular Courses & Classes

ISEE Courses & Classes in Phoenix, GRE Courses & Classes in Boston, MCAT Courses & Classes in New York City, GMAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in San Diego, GMAT Courses & Classes in Seattle, SAT Courses & Classes in Atlanta, ACT Courses & Classes in Seattle

Popular Test Prep

MCAT Test Prep in New York City, SSAT Test Prep in Miami, ISEE Test Prep in San Francisco-Bay Area, LSAT Test Prep in Phoenix, MCAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Seattle, ACT Test Prep in Boston, GMAT Test Prep in Los Angeles, SAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

MAP 7th Grade Math : Geometry

Study concepts, example questions & explanations for MAP 7th Grade Math

All MAP 7th Grade Math Resources

Example Questions

Example Question #1 : Geometry

Example Question #2 : Geometry

Example Question #3 : Geometry

All MAP 7th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: