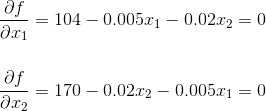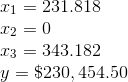All Math Modeling Resources
Example Questions
Example Question #1 : Intro To Probability Models
A beauty supply company manufactures a variety of brushes. Quality control engineers work to ensure that the defected brushes in the factory will be detected prior to shipping them. It is estimated that approximately 0.2% of the brushes made will be defected. Tests can be done individually on the brushes or on batches of the brushes. If the test on a batch of brushes fails, it means that one or more of the brushes in that particular batch are defected. The estimated cost is 4 cents for a single brush, and 

By testing brush batches in groups of 9 will reduce testing costs without sacrificing the quality.
By testing brush batches in groups of 15 will reduce testing costs without sacrificing the quality.
By testing brush batches in groups of 20 will reduce testing costs without sacrificing the quality.
By testing brush batches in groups of 10 will reduce testing costs without sacrificing the quality.
By testing brush batches in groups of 12 will reduce testing costs without sacrificing the quality.
By testing brush batches in groups of 15 will reduce testing costs without sacrificing the quality.
First identify the known variables and assumptions.
If
If a batch of brushes is tested and if the test shows that all the brushes are good then,
If the batch test shows that there is a defected brush in the batch then,
Use a discrete probability model to find the most cost-effected quality control procedure for detecting defected brushes.
Consider the random variable
that has a probability of
If the probability of a brush being good is 


Now there are 



Therefore the expected value of the random variable 
Therefore the average testing cost is,
Using the law of large numbers minimizing 
Now answer the question.
By testing brush batches in groups of 15 will reduce testing costs without sacrificing the quality.
Example Question #1 : Math Modeling
An oil spill occurs at a factory 12 kilometers up stream from a town. One hour after the spill happens it reaches the stream and a 1600 meters long patch of oil begins to flow towards the town at a rate of 2 kilometers per hour. The maximum concentration of the oil in the water is 15 times the acceptable level. What is the maximum concentration expected in town and when will it arrive?
Identify what is known and the assumptions.
This is a diffusion problem and thus a diffusion equation will be used with a term of relative concentration.
The relative concentration is denoted as
This function has been normalized resulting in the following.
The law of conservation of mass will also be useful is solving this problem.
The goal is to calculate the maximum pollution level in town.
The diffusion equation is,
Using the Fourier transforms to solve the diffusion equation is as follows.
For this particular function
so the interval will be
Calculate 
Now find where the maximum occurs in time.
Example Question #1 : Probability Models
A computer company has one service repair man and has space for 29 computers in the shop at one time. Last year the shop repaired 67 computers with an average repair time of 2 days per computer. Formulate a Markov process model for 


Using Markov Process for this question assume that the space is finite.
The stochastic process which determines the future of the process from a probabilistic standpoint is defined as follows.
Let
Recall that the exponential distribution, and thus the 
Now formulate the Markov Process specifically for this problem.
The transitions of computers in and out of the shop are,


Now calculate the rates up and down.
To calculate 

Its key to know that at zero we cannot move down a state and like wise when at 29, we cannot move up a state.
Solving with
Continuing in this fashion results in the following.
Now, writing the sum of a finite geometric series is
Now
therefore,
Next,
Example Question #1 : Math Modeling
A computer company has one service repair man and has space for 32 computers in the shop at one time. Last year the shop repaired 71 computers with an average repair time of 3 days per computer. Formulate a Markov process model for 


Using Markov Process for this question assume that the space is finite.
The stochastic process which determines the future of the process from a probabilistic standpoint is defined as follows.
Let
Recall that the exponential distribution, and thus the 
Now formulate the Markov Process specifically for this problem.
The transitions of computers in and out of the shop are,


Now calculate the rates up and down.
To calculate 

Its key to know that at zero we cannot move down a state and like wise when at 29, we cannot move up a state.
Solving with
Continuing in this fashion results in the following.
Now, writing the sum of a finite geometric series is
Now
therefore,
Next,
Example Question #1 : Probability Models
A computer company has one service repair man and has space for 23 computers in the shop at one time. Last year the shop repaired 51 computers with an average repair time of 5 days per computer. Formulate a Markov process model for 


Using Markov Process for this question assume that the space is finite.
The stochastic process which determines the future of the process from a probabilistic standpoint is defined as follows.
Let
Recall that the exponential distribution, and thus the 
Now formulate the Markov Process specifically for this problem.
The transitions of computers in and out of the shop are,


Now calculate the rates up and down.
To calculate 

Its key to know that at zero we cannot move down a state and like wise when at 29, we cannot move up a state.
Solving with
Continuing in this fashion results in the following.
Now, writing the sum of a finite geometric series is
Now
therefore,
Next,
Example Question #1 : One Variable Optimization
A cow that weighs 175 pounds gains 3 pounds per day, and it costs 30 cents per day to keep that cow. The market price for cows is 75 cents per pound, but the price is falling one cent per day. When should the cow be sold to make the maximum profit?
Use the 5-step method.
The cow should be sold after 4 days.
The cow should be sold after 2 days.
The cow should be sold after 3 days.
The max profit is $131.58.
The max profit is $151.58.
The cow should be sold after 3 days.
The 5-step method for this particular modeling question is as follows.
1. Ask the question
When should the cow be sold to make the maximum profit?
Now identify all known information.
Variables:
2. Select the modeling approach
For this particular question the function can be define 

3. Formulate the model
To maximize 

Now rewrite the equation in terms of 
4. Solve the model
Now to solve the model, take the derivative, set it equal to zero, and solve for 
5. Answer the question
The cow should be sold after 3 days.
Example Question #1 : Multivariable Optimization
A company that makes computer monitors is unveiling two new products this spring, a 15 inch screen for $189 and a 19 inch screen for $269. The cost to manufacture the 15 inch screens is $85 per screen and the 19 inch screen is $99 per screen, plus $200,000 for miscellaneous costs. The number of sells for each screen type effects the average selling price. It is estimated that each set average selling price drops by two cents for each additional screen sold. The average sells price for the 15 inch screen will decrease by 0.2 cents for each 19 inch screen sold, the price of the 19 inch screen decreases by 0.3 cents for each 15 inch screen sold. What are the partial differential equations used to find how many units of each type of screens should be manufactured to optimize profit?
First, identify all known information.
Variables:
Assumptions:

Objective:
Maximize the profit.
Theorem: If 





Therefore, to find the maximum point in this function, simultaneously solve the differential equations in question and check the boundary points.
Now switch variables/
Over
From here take the partial differential equation of each variable. Since the questioned asked for the partial differential equations that would be used to optimize the profit we can stop here.
Example Question #2 : Math Modeling
Using Newton's Method as the computational method, optimize the follow problem.
A cow that weighs 175 pounds gains 3 pounds per day, and it costs 30 cents per day to keep that cow. The market price for cows is 75 cents per pound, but the price is falling one cent per day. When should the cow be sold to make the maximum profit?
It is recommended to wait 6 or 7 days to sell the cow. This should result in a net profit of $130.
It is recommended to wait 9 or 10 days to sell the cow. This should result in a net profit of $132.
It is recommended to wait 8 or 9 days to sell the cow. This should result in a net profit of $132.90.
It is recommended to wait 2 or 5 days to sell the cow. This should result in a net profit of $131.90.
It is recommended to wait 7 or 8 days to sell the cow. This should result in a net profit of $131.90.
It is recommended to wait 7 or 8 days to sell the cow. This should result in a net profit of $131.90.
Assume that the growth rate of the cow is proportional to its weight.
In mathematical terms:
Looking at the known information,
Variables:
Therefore,

when
Thus the differential equation to solve for 
Solving by separation of variables results in the following equation.
From here, formulate the model with the new weight equation.
Recall that the goal is to optimize the question over

Use a graphing calculator or computer technology to graph the function.

Observing the graph it appears the maximum profit for the cow occurs around 

From here, answer the question. Taking into account the growth rate of the cow is still increasing, it is recommended to wait 7 or 8 days to sell the cow. This should result in a net profit of $131.90.
Example Question #3 : Math Modeling
A farm has 750 acres of land available for planting crops. The possible crops are soy, corn, and oats. There is 1,200 acre-ft of water for irrigation and the crew will be able to work of the farm 575 hours per week.
Find the amount of each crop that should be planted to maximize the profit.
The table below includes some additional, helpful information.
The objective of this particular problem is to maximize the profit.
Maximize the function:
over the region defined by the constraints.
First identify the variables and assumptions of the problem.

Now using the constraints formulate the linear programming model.
From here use computer implementation to solve using the simplex method.
Therefore, the optimal solution will occur when there are 510 acres of soy planted and 65 acres of oats.
The maximum profit at this solution will be, $223,500.
Example Question #3 : Math Modeling
A farm has 750 acres of land available for planting crops. The possible crops are soy, corn, and oats. There is 1,200 acre-ft of water for irrigation and the crew will be able to work of the farm 575 hours per week.
Find the amount of each crop that should be planted to maximize the profit.
The table below includes some additional, helpful information.
The objective of this particular problem is to maximize the profit.
Maximize the function:
over the region defined by the constraints.
First identify the variables and assumptions of the problem.

Now using the constraints formulate the linear programming model.
From here use computer implementation to solve using the simplex method.
Therefore, the optimal solution will occur when there are 343.182 acres of soy planted and 231.818 acres of corn planted.
The maximum profit at this solution will be, $230,454.50.
All Math Modeling Resources








](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012889/gif.latex)
 \\EC=(3+n)+4n(1-0.998^n) \\EC=3+5n-4n(0.998^n)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012895/gif.latex)



















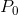














![[\text{Rate In}]=[\text{Rate Out}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1013040/gif.latex)