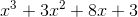Pre-Algebra : Polynomials
Study concepts, example questions & explanations for Pre-Algebra
All Pre-Algebra Resources
Example Questions
Example Question #1 : Adding And Subtracting Polynomials
Simplify:
Combine like terms:
Example Question #2 : Adding And Subtracting Polynomials
Simplify:
You can first rewrite the problem without the parentheses:
Next, write the problem so that like terms are next to eachother:
Then, add or subtract (depending on the operation) like terms. Remember that variables with different exponents are not like terms. For example, 
Example Question #3 : Polynomials
Simplify:
When subtracting one polynomial from another, you must use distributive property to distribute the – sign:
Now, rewrite the entire problem without the parentheses:
Reorganize the problem so that like terms are together. Remember that variables with different exponents are not like terms. For example, 
Combine the like terms by adding or subtracting (depending on the operation):
Example Question #4 : Polynomials
Simplify:
First simplify the parentheses to get:
Then combine like terms to get your answer of
Example Question #4 : Adding And Subtracting Polynomials
Simplify the expression:
To simplify the expression, combine like terms and eliminate the parentheses. Start by distributing the negative through the second parentheses.
Next, combine like terms.
Example Question #3 : Adding And Subtracting Polynomials
Simplify the following expression:
In previous problems, we used combining like terms to simplify. In this case, we first need to distribute in order to get rid of the parentheses.
Parentheses always indicate the operation multiplication. You multiply the number on the ouside of the parenthese by EVERY term inside the parentheses. In this case, you would multiply 
After this first step, you should have:
Then, we will combine like terms. Here, the like terms are 
So the final answer is
Example Question #3 : Adding And Subtracting Polynomials
Simplify the following expression:
In previous problems, we used combining like terms to simplify. In this case, we first need to distribute in order to get rid of the parentheses.
Parentheses always indicate the operation multiplication. You multiply the number on the ouside of the parenthese by EVERY term inside the parentheses. In this case, you would multiply 
After this first step, you should have:
Then, we will combine like terms. Here, the like terms are 
So the final answer is
(There is not anything you need to combine the 12 with, so you just leave it as is.)
Example Question #5 : Adding And Subtracting Polynomials
Simplify the following expression:
In previous problems, we used combining like terms to simplify. In this case, we first need to distribute in order to get rid of the parentheses.
Parentheses always indicate the operation multiplication. You multiply the number on the ouside of the parenthese by EVERY term inside the parentheses. In this case, you would multiply 
After this first step, you should have:
Then, we will combine like terms. Here, the like terms are 
So the final answer is
Example Question #5 : Adding And Subtracting Polynomials
Simplify the following expression:
The simplify this expression, combine like terms. Terms are like if they have the same variables and powers. To combine them, use addition and/or subtraction of the coefficients. The variables and powers do not change when you are combining.
So 
So the answer is:
Example Question #4 : Polynomials
Simplify the following expression:
The simplify this expression, combine like terms. Terms are like if they have the same variables and powers. To combine them, use addition and/or subtraction of the coefficients. The variables and powers do not change when you are combining.
So
So the answer is:
All Pre-Algebra Resources
