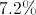How to calculate the amount of sales tax?

1.      Convert tax percentage into a decimal by moving the decimal point two spaces to the left.
2.      Multiple the pre-tax value by the newly calculated decimal value in order to find the cost of the sales tax.
3.      Add the sales tax value to the pre-tax value to calculate the total cost.

Calculating sales tax at time of purchase:

In order to calculate the sales tax of an item, we need to first multiply the pre-tax cost of the item by the sales tax percentage after it has been converted into a decimal. Once the sales tax has been calculated it needs to be added to the pre-tax value in order to find the total cost of the item. Let's start by working with an example. If a magazine costs $2.35 and has a 6% sales tax, then what is the total cost of the item. First, we need to convert the sales tax percentage into a decimal by moving the point two spaces to the left.

Now, we need to multiply the pre-tax cost of this item by this value in order to calculate the sales tax cost.

Round to two decimal places since our total is in dollars and cents.

Last, add this value to the pre-tax value of the item to find the total cost.

Calculating the sales tax percentage of a total:

If we are given the total cost of an item or group of items and the pre-tax cost of the good(s), then we can calculate the sales tax percentage of the total cost. First, we need to subtract the pre-tax value from the total cost of the purchase. Next, we need to create a ratio of the sales tax to the pre-tax cost off the items. Last, we need to create a proportion where the pre-tax cost is related to 100% and solve for the percentage of the sales tax. Let's start by working through an example. If a person pays $245.64 for groceries that cost $220.00 pre tax, then what is the sales tax percentage for the items.

First, subtract the pre-tax value from the total cost of the items to find the sales tax cost.

Next, create a ratio of the sales tax to the pre-tax cost of the items.

Last, create a proportion where the pre-tax value is proportional to 100% and solve for the percentage of sales tax.

Cross multiply and solve.

Isolate the sales tax percentage to the left side of the equation by dividing each side by the pre-tax value.

Round to two decimal places since our answer is in dollars and cents.

Last, we can check this answer by calculating the sales tax percentage of the total as seen previously.

First, we need to convert the sales tax percentage into a decimal by moving the point two spaces to the left.

Now, we need to multiply the pre-tax cost of this item by this value in order to calculate the sales tax cost.

Round to two decimal places since our total is in dollars and cents.

Last, add this value to the pre-tax value of the item to find the total cost.

Our answers check out; therefore they are correct. Now, let's use this information to solve the given problem.

Solution: 

If each soda cost $1.56 and Jane bought four, the total for the sodas was:

And she paid $6.93

The sales tax was 11%.

 is the cube of , which is the difference of twelve and a number. Therefore,  is "the cube of the difference of twelve and a number."

This question involves muliple steps to attain the correct answer.

To solve for the weight of the bucket (we will let 'x' represent this) the following equation can be set up:

To isolate x, subtract 9 * 1.22 (which is equal to 10.98) from both sides. We find x to be equal to 2.32.

The question asks us for the percentage of the total weight, so to find this, we must divide 2.32 by the total weight and multiple our answer by 100.

Rounded to two decimal points of accuracy, the final answer is 17.44%.

 is the square root of ,which is the difference of a number and eighteen; therefore,  is "the square root of the difference of a number and eighteen".

 is nine less than , which is the reciprocal of a number. Therefore,  is "nine less than the reciprocal of a number. "

 is the square of the expression ;  is the difference of eight and a number.

Subsequently,  is "the square of the difference of eight and a number".

Since you are solving for , that goes on one side of the equation.   and 's revenues are based on how much they sell for per pound.  

So for every pound of apples they make  dollars or .  

For every pound of oranges they make  dollars or .  

To put it all together, you get 

.

Sam starts out with five ducks. He receives 3 ducks after every two months.

where .

After the first 2 months, he will have 8 ducks.

After the next 2 months, he will have 11 ducks.

After the next 2 months, he will then have 14 ducks.

However, Sam will not receive 3 ducks until the 8th month. This means that he will only have 14 ducks in possession by the 7th month.

The answer is: