All SAT II Math I Resources
Example Questions
Example Question #1 : Range And Domain
Define 
Give the range of 
The radicand within a square root symbol must be nonnegative, so
This happens if and only if 

![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218954/gif.latex)


![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218957/gif.latex)


Similarly, 

![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218963/gif.latex)


Therefore, the range of 
![[0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218969/gif.latex)
Example Question #1 : Range And Domain
Define 
Give the domain of 
The radicand within a square root symbol must be nonnegative, so
This happens if and only if 

![[-4,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218946/gif.latex)
Example Question #1 : Range And Domain
Define the functions 

Give the natural domain of the composite function 
The set of all real numbers
The set of all real numbers
The natural domain of the composite function 
One set is the natural domain of 

The other set is the set of all values of 





Therefore, the other set is the set of all 
Substitute:
This holds for all real numbers, so this set is also the set of all real numbers.
The natural domain of 
Example Question #2 : Range And Domain
Domain: All real numbers
Range:
Domain: All real numbers
Range:
Domain: All real numbers
Range:
The domain includes the values that go into a function (the x-values) and the range are the values that come out (the 


Example Question #3 : Range And Domain
Which of the following is NOT a function?
A function has to pass the vertical line test, which means that a vertical line can only cross the function one time. To put it another way, for any given value of 












Example Question #1 : Functions And Graphs
Give the domain of the function below.

The domain is the set of possible value for the 

Now we can solve for 
There is no real value of 
The radicand is always positive, and 


Example Question #1 : Properties Of Functions And Graphs
Find the domain:
To find the domain, find all areas of the number line where the fraction is defined.

Factor by finding two numbers that sum to -2 and multiply to 1. These numbers are -1 and -1.
Example Question #363 : Algebra Ii
If 

Using 



Therefore 

Example Question #5 : Range And Domain
What is the range of the function?
This function is a parabola that has been shifted up five units. The standard parabola has a range that goes from 0 (inclusive) to positive infinity. If the vertex has been moved up by 5, this means that its minimum has been shifted up by five. The first term is inclusive, which means you need a "[" for the beginning.
Minimum: 5 inclusive, maximum: infinity
Range:
Example Question #1 : Domain And Range
What is the domain of the function?
The domain represents the acceptable 
Minimum: 0 inclusive, maximum: infinity
Domain:
Certified Tutor
Certified Tutor
All SAT II Math I Resources

![[0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218892/gif.latex)
![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218894/gif.latex)
![(-\infty, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218898/gif.latex)
![[0, 25]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218893/gif.latex)
![[-25,25]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218896/gif.latex)






![[0, 4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218873/gif.latex)
![(-\infty, 4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218875/gif.latex)
![[-4,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218872/gif.latex)















 is a sine curve. What are the domain and range of this function?
is a sine curve. What are the domain and range of this function?























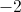














![[0,100]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218211/gif.latex)







