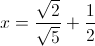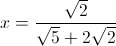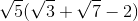All SAT Math Resources
Example Questions
Example Question #1 : Basic Squaring / Square Roots
Solve for 
Notice how all of the quantities in square roots are divisible by 9
Simplifying, this becomes
Example Question #1 : Basic Squaring / Square Roots
Solve for 
Note that all of the square root terms share a common factor of 36, which itself is a square of 6:
Factoring 
Example Question #2 : Basic Squaring / Square Roots
Solve for 
Note that both 



From here, we can factor 
Example Question #1 : How To Find The Common Factor Of Square Roots
Solve for 
In order to solve for 
Simplifying, this becomes:
Example Question #1 : Factoring Common Factors Of Squares And Square Roots
Which of the following is equivalent to:

To begin with, factor out the contents of the radicals. This will make answering much easier:
They both have a common factor 
This is the same as:
These have a common 
Example Question #1 : How To Find The Common Factor Of Square Roots
Simplify:
These three roots all have a 
Now, this could be rewritten:
Now, note that
Therefore, you can simplify again:
Now, that looks messy! Still, if you look carefully, you see that all of your factors have 
This is the same as:
Example Question #4 : Basic Squaring / Square Roots
Solve for 
Examining the terms underneath the radicals, we find that 







The equation can then be expressed in terms of these factored radicals as shown:


Factoring the common term 
Divide both sides by the expression in the parentheses:
Divide both sides by 

Simplify the fraction on the righthand side by dividing the numerator and denominator by 
This is the solution for the unknown variable 
Example Question #1 : How To Multiply Square Roots
Simplify:
When multiplying square roots, you are allowed to multiply the numbers inside the square root. Then simplify if necessary.
Example Question #1 : How To Multiply Square Roots
Simplify:
When multiplying square roots, you are allowed to multiply the numbers inside the square root. Then simplify if necessary.
Example Question #1 : How To Multiply Square Roots
Simplify:
When multiplying square roots, you are allowed to multiply the numbers inside the square root. Then simplify if necessary.
Certified Tutor
Certified Tutor
All SAT Math Resources