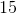Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : How to find the length of the side of a right triangle

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #671 : Ssat Upper Level Quantitative (Math)

A right triangle has a hypotenuse of 39 and one leg is 36. What is the length of the other leg?

Possible Answers:

$\displaystyle 19$

$\displaystyle 3$

$\displaystyle 33$

$\displaystyle 27$

$\displaystyle 15$

Correct answer:

$\displaystyle 15$

Explanation:

You may recognize these numbers as multiples of 13 and 12 (each by a factor of 3) and remember that sides of length 5, 12 and 13 make a special right triangle. So the other leg would be 15 $(5\times 3)$ $\displaystyle (5\times 3)$.

If you don't remember this, you can use Pythagorean theorem:

$39^{2}-36^{2}= 1521-1296=225$ $\displaystyle 39^{2}-36^{2}= 1521-1296=225$

$\sqrt{225}=15$ $\displaystyle \sqrt{225}=15$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

A right triangle has a hypotenuse of $\displaystyle 12$ and one leg has a length of $\displaystyle 9$. What is the length of the other leg?

Possible Answers:

$\displaystyle 11$

$\displaystyle 8$

$7\sqrt{3}$ $\displaystyle 7\sqrt{3}$

$\displaystyle 10$

$3\sqrt{7}$ $\displaystyle 3\sqrt{7}$

Correct answer:

$3\sqrt{7}$ $\displaystyle 3\sqrt{7}$

Explanation:

When calculating the lengths of sides of a right triangle, we can use the Pythagorean Theorem as follows:

$a^{2}+b^{2}=c^{2}$ $\displaystyle a^{2}+b^{2}=c^{2}$, where $\displaystyle a$ and $\displaystyle b$ are legs of the triangle and $\displaystyle c$ is the hypotenuse.

Plugging in our given values:

$9^{2}+b^{2}=12^{2}$ $\displaystyle 9^{2}+b^{2}=12^{2}$

Subtracting 9^2 $\displaystyle 9^2$ from each side of the equation:

$b^{2}=12^{2}-9^{2}$ $\displaystyle b^{2}=12^{2}-9^{2}$

$b^{2}=144-81$ $\displaystyle b^{2}=144-81$

$b^{2}=63$ $\displaystyle b^{2}=63$

Taking the square root of each side of the equation:

$b=\sqrt{63}$ $\displaystyle b=\sqrt{63}$

Simplifying the square root:

$b=\sqrt{9\times 7}$ $\displaystyle b=\sqrt{9\times 7}$

$b=3\sqrt{7}$ $\displaystyle b=3\sqrt{7}$

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

A right triangle has two legs of length $\displaystyle 6$ and $\displaystyle 10$, respectively. What is the hypotenuse of the right triangle?

Possible Answers:

$\displaystyle 12$

$2\sqrt{17}$ $\displaystyle 2\sqrt{17}$

$2\sqrt{34}$ $\displaystyle 2\sqrt{34}$

$17\sqrt{2}$ $\displaystyle 17\sqrt{2}$

$34\sqrt{2}$ $\displaystyle 34\sqrt{2}$

Correct answer:

$2\sqrt{34}$ $\displaystyle 2\sqrt{34}$

Explanation:

When calculating the lengths of sides of a right triangle, we can use the Pythagorean Theorem as follows:

$a^{2}+b^{2}=c^{2}$ $\displaystyle a^{2}+b^{2}=c^{2}$, where $\displaystyle a$ and $\displaystyle b$ are legs of the triangle and $\displaystyle c$ is the hypotenuse.

Plugging in our given values:

$6^{2}+10^{2}=c^{2}$ $\displaystyle 6^{2}+10^{2}=c^{2}$

$36+100=c^{2}$ $\displaystyle 36+100=c^{2}$

$136=c^{2}$ $\displaystyle 136=c^{2}$

$\sqrt{136}=c$ $\displaystyle \sqrt{136}=c$

$\sqrt{17\times 8}=c$ $\displaystyle \sqrt{17\times 8}=c$

$\sqrt{17\times 4\times 2}=c$ $\displaystyle \sqrt{17\times 4\times 2}=c$

$2\sqrt{34}=c$ $\displaystyle 2\sqrt{34}=c$

Report an Error

Example Question #3 : How To Find The Length Of The Side Of A Right Triangle

A right triangle has a leg of length $\displaystyle 7$ and a hypotenuse of length $\displaystyle 11$. What is the length of the other leg?

Possible Answers:

$2\sqrt{6}$ $\displaystyle 2\sqrt{6}$

$6\sqrt{2}$ $\displaystyle 6\sqrt{2}$

$9\sqrt{6}$ $\displaystyle 9\sqrt{6}$

$6\sqrt{9}$ $\displaystyle 6\sqrt{9}$

$\displaystyle 9$

Correct answer:

$6\sqrt{2}$ $\displaystyle 6\sqrt{2}$

Explanation:

When calculating the lengths of sides of a right triangle, we can use the Pythagorean Theorem as follows:

$a^{2}+b^{2}=c^{2}$ $\displaystyle a^{2}+b^{2}=c^{2}$, where $\displaystyle a$ and $\displaystyle b$ are legs of the triangle and $\displaystyle c$ is the hypotenuse.

Plugging in our given values:

$7^{2}+b^{2}=11^{2}$ $\displaystyle 7^{2}+b^{2}=11^{2}$

Subtracting 7^2 $\displaystyle 7^2$ from each side of the equation:

$b^{2}=11^{2}-7^{2}$ $\displaystyle b^{2}=11^{2}-7^{2}$

$b^{2}=121-49$ $\displaystyle b^{2}=121-49$

$b^{2}=72$ $\displaystyle b^{2}=72$

$b=\sqrt{72}$ $\displaystyle b=\sqrt{72}$

$b=\sqrt{36\times 2}$ $\displaystyle b=\sqrt{36\times 2}$

$b=6\sqrt{2}$ $\displaystyle b=6\sqrt{2}$

Report an Error

Example Question #11 : Properties Of Triangles

Find the length of the missing side.

Possible Answers:

160 $\displaystyle 160$

$4\sqrt{10}$ $\displaystyle 4\sqrt{10}$

$\sqrt{15}$ $\displaystyle \sqrt{15}$

$\displaystyle 80$

Correct answer:

$4\sqrt{10}$ $\displaystyle 4\sqrt{10}$

Explanation:

Use the Pythagorean Theorem to find the length of the missing side.

$\displaystyle x^2+6^2=14^2$

$\displaystyle x^2+36=196$

x^2=160 $\displaystyle x^2=160$

$x=\sqrt{160}=4\sqrt{10}$ $\displaystyle x=\sqrt{160}=4\sqrt{10}$

Report an Error

Example Question #12 : Properties Of Triangles

Find the length of the missing side.

Possible Answers:

176 $\displaystyle 176$

$8\sqrt2$ $\displaystyle 8\sqrt2$

$4\sqrt{13}$ $\displaystyle 4\sqrt{13}$

$4\sqrt{11}$ $\displaystyle 4\sqrt{11}$

Correct answer:

$4\sqrt{11}$ $\displaystyle 4\sqrt{11}$

Explanation:

Use the Pythagorean Theorem to find the length of the missing side.

$\displaystyle x^2+7^2=15^2$

$\displaystyle x^2+49=225$

x^2=176 $\displaystyle x^2=176$

$x=\sqrt{176}=4\sqrt{11}$ $\displaystyle x=\sqrt{176}=4\sqrt{11}$

Report an Error

Example Question #11 : Right Triangles

Find the length of the missing side.

Possible Answers:

$\displaystyle 4$

$\displaystyle 5$

$\displaystyle 25$

$\displaystyle 8$

Correct answer:

$\displaystyle 5$

Explanation:

Use the Pythagorean Theorem to find the length of the missing side.

$\displaystyle x^2+12^2=13^2$

$\displaystyle x^2+144=169$

x^2=25 $\displaystyle x^2=25$

$x=\sqrt{25}=5$ $\displaystyle x=\sqrt{25}=5$

Report an Error

Example Question #12 : Right Triangles

Find the length of the missing side.

Possible Answers:

$\displaystyle 12$

$\displaystyle 10$

100 $\displaystyle 100$

$\displaystyle 14$

Correct answer:

$\displaystyle 10$

Explanation:

Use the Pythagorean Theorem to find the length of the missing side.

$\displaystyle x^2+24^2=26^2$

$\displaystyle x^2+576=676$

x^2=100 $\displaystyle x^2=100$

$x=\sqrt{100}=10$ $\displaystyle x=\sqrt{100}=10$

Report an Error

Example Question #13 : Right Triangles

Find the length of the missing side.

Possible Answers:

$\displaystyle 8$

$\displaystyle 64$

$\displaystyle 9$

$\displaystyle 5$

Correct answer:

$\displaystyle 8$

Explanation:

Use the Pythagorean Theorem to find the length of the missing side.

$\displaystyle x^2+6^2=10^2$

$\displaystyle x^2+36=100$

x^2=64 $\displaystyle x^2=64$

$x=\sqrt{64}=8$ $\displaystyle x=\sqrt{64}=8$

Report an Error

Example Question #14 : Right Triangles

Find the length of the missing side.

Possible Answers:

300 $\displaystyle 300$

$\displaystyle 20$

$10\sqrt3$ $\displaystyle 10\sqrt3$

$10\sqrt5$ $\displaystyle 10\sqrt5$

Correct answer:

$10\sqrt3$ $\displaystyle 10\sqrt3$

Explanation:

Use the Pythagorean Theorem to find the length of the missing side.

$\displaystyle x^2+10^2=20^2$

$\displaystyle x^2+100=400$

x^2=300 $\displaystyle x^2=300$

$x=\sqrt{300}=10\sqrt{3}$ $\displaystyle x=\sqrt{300}=10\sqrt{3}$

Report an Error

View SSAT- Upper Level Tutors

Calvin
Certified Tutor

University of Southern California, Bachelor of Science, International Relations.

View SSAT- Upper Level Tutors

Iffy
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Computer Engineering, General. University of Maryland-College P...

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Seattle, GMAT Tutors in Seattle, ACT Tutors in Denver, SSAT Tutors in Miami, SSAT Tutors in Houston, MCAT Tutors in Atlanta, Algebra Tutors in Philadelphia, Math Tutors in Denver, Calculus Tutors in San Diego, ACT Tutors in Philadelphia

Popular Courses & Classes

ACT Courses & Classes in San Diego, SSAT Courses & Classes in Phoenix, MCAT Courses & Classes in New York City, GRE Courses & Classes in Washington DC, LSAT Courses & Classes in Phoenix, Spanish Courses & Classes in Denver, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in Philadelphia, ISEE Courses & Classes in Washington DC, GRE Courses & Classes in Seattle

Popular Test Prep

SSAT Test Prep in Dallas Fort Worth, SAT Test Prep in Miami, MCAT Test Prep in New York City, GRE Test Prep in Atlanta, GRE Test Prep in Seattle, ISEE Test Prep in San Francisco-Bay Area, SSAT Test Prep in San Diego, ACT Test Prep in Dallas Fort Worth, MCAT Test Prep in Miami, SAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : How to find the length of the side of a right triangle

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #671 : Ssat Upper Level Quantitative (Math)

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

Example Question #3 : How To Find The Length Of The Side Of A Right Triangle

Example Question #11 : Properties Of Triangles

Example Question #12 : Properties Of Triangles

Example Question #11 : Right Triangles

Example Question #12 : Right Triangles

Example Question #13 : Right Triangles

Example Question #14 : Right Triangles

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: