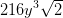We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : How to find the volume of a polyhedron

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Volume Of A Polyhedron

Find the volume of a square pyramid that has a height of and a side length of .

Possible Answers:

Correct answer:

Explanation:

The formula to find the volume of a square pyramid is

$\text{Volume}=(side)^2\frac{height}{3}$

So plugging in the information given from the question,

$\text{Volume}=4^2\frac{9}{3}=16\times3=48$

Report an Error

Example Question #2 : How To Find The Volume Of A Polyhedron

Find the volume of a square pyramid with a height of and a length of a side of its square base of .

Possible Answers:

Correct answer:

Explanation:

The formula to find the volume of a square pyramid is

$\text{Volume}=(side)^2\frac{height}{3}$

So plugging in the information given from the question,

$\text{Volume}=(3^2)\frac{12}{3}=9\times 4=36$

Report an Error

Example Question #3 : How To Find The Volume Of A Polyhedron

Find the volume of a regular hexagonal prism that has a height of . The side length of the hexagon base is .

Possible Answers:

$1440\sqrt3$

$4320\sqrt3$

$2160\sqrt3$

$660\sqrt3$

Correct answer:

$2160\sqrt3$

Explanation:

The formula to find the volume of a hexagonal prism is

$\text{Volume}=\frac{3\sqrt3}{2}(side)^2(height)$

Plugging in the values given by the question will give

$\text{Volume}=\frac{3\sqrt3}{2}(12^2)(10)=2160\sqrt3$

Report an Error

Example Question #22 : Volume Of A Three Dimensional Figure

In terms of , find the volume of a regular hexagonal prism that has a height of . The hexagon base has side lengths of .

Possible Answers:

$240x\sqrt3$

$120x\sqrt3$

$360x^2\sqrt3$

$120x^2\sqrt3$

Correct answer:

$120x^2\sqrt3$

Explanation:

The formula to find the volume of a hexagonal prism is

$\text{Volume}=\frac{3\sqrt3}{2}(side)^2(height)$

Plugging in the values given by the question will give

$\text{Volume}=\frac{3\sqrt3}{2}(4x)^2(5)=120x^2\sqrt3$

Report an Error

Example Question #4 : How To Find The Volume Of A Polyhedron

Find the volume of a regular tetrahedron with a side length of .

Possible Answers:

$144\sqrt2$

$966\sqrt2$

$288\sqrt2$

$1728\sqrt2$

Correct answer:

$144\sqrt2$

Explanation:

The formula to find the volume of a tetrahedron is

$\text{Volume}=\frac{\sqrt2}{12}(side)^3$

Plugging in the information given by the question gives

$\text{Volume}=\frac{\sqrt2}{12}(12)^3=144\sqrt2$

Report an Error

Example Question #5 : How To Find The Volume Of A Polyhedron

Find the volume of a regular octahedron that has a side length of .

Possible Answers:

$100\sqrt2$

$\frac{500\sqrt2}{3}$

$\frac{512\sqrt2}{3}$

$512\sqrt2$

Correct answer:

$\frac{512\sqrt2}{3}$

Explanation:

Use the following formula to find the volume of a regular octahedron:

$\text{Volume}=\frac{\sqrt2}{3}(side)^3$

Plugging in the information from the question,

$\text{Volume}=\frac{\sqrt2}{3}(8)^3=\frac{512\sqrt2}{3}$

Report an Error

Example Question #6 : How To Find The Volume Of A Polyhedron

Find the volume of a regular octahedron that has a side length of .

Possible Answers:

$84y^3\sqrt2$

$144y^3\sqrt2$

$216y^3\sqrt2$

$72y^3\sqrt2$

Correct answer:

$72y^3\sqrt2$

Explanation:

Use the following formula to find the volume of a regular octahedron:

$\text{Volume}=\frac{\sqrt2}{3}(side)^3$

Plugging in the information from the question,

$\text{Volume}=\frac{\sqrt2}{3}(6y)^3=72y^3\sqrt2$

Report an Error

Example Question #31 : Volume Of A Three Dimensional Figure

Find the volume of a regular hexahedron with a side length of .

Possible Answers:

196

$1372\sqrt3$

2744

$\frac{2744\sqrt2}{3}$

Correct answer:

2744

Explanation:

A regular hexahedron is another name for a cube.

To find the volume of a cube,

$\text{Volume}=(side)^3$

Plugging in the information given in the question gives

$\text{Volume}=(14)^3=2744$

Report an Error

Example Question #32 : Volume Of A Three Dimensional Figure

Find the volume of a regular octahedron with side lengths of .

Possible Answers:

$243t^3\sqrt2$

$243t\sqrt2$

$729t^3\sqrt2$

$81t^3\sqrt2$

Correct answer:

$243t^3\sqrt2$

Explanation:

Use the following formula to find the volume of a regular octahedron:

$\text{Volume}=\frac{\sqrt2}{3}(side)^3$

Plugging in the information from the question,

$\text{Volume}=\frac{\sqrt2}{3}(9t)^3=243t^3\sqrt2$

Report an Error

Example Question #33 : Volume Of A Three Dimensional Figure

Find the volume of a prism that has a right triangle base with leg lengths of and and a height of .

Possible Answers:

432

288

144

Correct answer:

144

Explanation:

To find the volume of a prism, multiply the area of the base by the height.

$\text{Area of Base}=\frac{3\times8}{2}=12$

$\text{Volume}=12\times height=12\times12=144$

Report an Error

View SSAT- Upper Level Tutors

Chase
Certified Tutor

Western Governors University, Bachelor of Science, Mathematics.

View SSAT- Upper Level Tutors

Wardell
Certified Tutor

SIU Edwardsville, Bachelor in Arts, English.

View SSAT- Upper Level Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Denver, GMAT Tutors in San Diego, MCAT Tutors in Washington DC, ACT Tutors in Chicago, SSAT Tutors in Houston, ACT Tutors in Boston, Algebra Tutors in Atlanta, ISEE Tutors in Seattle, ACT Tutors in Miami, GRE Tutors in Phoenix

Popular Courses & Classes

ACT Courses & Classes in Atlanta, SSAT Courses & Classes in Miami, ACT Courses & Classes in Denver, LSAT Courses & Classes in Los Angeles, SAT Courses & Classes in Atlanta, SAT Courses & Classes in Boston, ISEE Courses & Classes in Los Angeles, GMAT Courses & Classes in Seattle, ACT Courses & Classes in Seattle, SAT Courses & Classes in Phoenix

Popular Test Prep

MCAT Test Prep in Seattle, LSAT Test Prep in Los Angeles, GMAT Test Prep in Seattle, MCAT Test Prep in Denver, MCAT Test Prep in Phoenix, ACT Test Prep in Denver, SSAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Miami, SSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : How to find the volume of a polyhedron

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #1 : How To Find The Volume Of A Polyhedron

Example Question #2 : How To Find The Volume Of A Polyhedron

Example Question #3 : How To Find The Volume Of A Polyhedron

Example Question #22 : Volume Of A Three Dimensional Figure

Example Question #4 : How To Find The Volume Of A Polyhedron

Example Question #5 : How To Find The Volume Of A Polyhedron

Example Question #6 : How To Find The Volume Of A Polyhedron

Example Question #31 : Volume Of A Three Dimensional Figure

Example Question #32 : Volume Of A Three Dimensional Figure

Example Question #33 : Volume Of A Three Dimensional Figure

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: