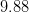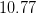Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Distance Formula

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #91 : Coordinate Geometry

A line segment has the endpoints (-1, 3) $\displaystyle (-1, 3)$ and (4,-2) $\displaystyle (4,-2)$. What is the length of this line segment?

Possible Answers:

$\displaystyle 5$

$\displaystyle 3$

$5\sqrt2$ $\displaystyle 5\sqrt2$

$\sqrt{30}$ $\displaystyle \sqrt{30}$

Correct answer:

$5\sqrt2$ $\displaystyle 5\sqrt2$

Explanation:

Use the following formula to find the distance between two points:

$\text{Distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle \text{Distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Plug in the points that are given.

$\text{Distance}=\sqrt{(4-(-1))^2+(-2-3)^2}$ $\displaystyle \text{Distance}=\sqrt{(4-(-1))^2+(-2-3)^2}$

$\text{Distance}=\sqrt{(5)^2+(-5)^2}$ $\displaystyle \text{Distance}=\sqrt{(5)^2+(-5)^2}$

$\text{Distance}=\sqrt{25+25}=\sqrt{50}=\sqrt{5*5*2}=5\sqrt2$ $\displaystyle \text{Distance}=\sqrt{25+25}=\sqrt{50}=\sqrt{5*5*2}=5\sqrt2$

Report an Error

Example Question #92 : Coordinate Geometry

A line segment has end points at (8,1) $\displaystyle (8,1)$ and (-2,-3) $\displaystyle (-2,-3)$. What is the length of this line segment?

Possible Answers:

9.88 $\displaystyle 9.88$

7.46 $\displaystyle 7.46$

6.32 $\displaystyle 6.32$

10.77 $\displaystyle 10.77$

Correct answer:

10.77 $\displaystyle 10.77$

Explanation:

The distance between two points is given by the following equation:

$\text{Distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle \text{Distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Now, using the two given points, plug them in to find the distance.

$\text{Distance}=\sqrt{(-2-8)^2+(-3-1)^2}=\sqrt{100+16}=\sqrt{116}=10.77$ $\displaystyle \text{Distance}=\sqrt{(-2-8)^2+(-3-1)^2}=\sqrt{100+16}=\sqrt{116}=10.77$

Report an Error

Example Question #371 : Ssat Upper Level Quantitative (Math)

Find the length of a line that has end points at $(8, -1)\text{ and }(-2, 1)$ $\displaystyle (8, -1)\text{ and }(-2, 1)$.

Possible Answers:

$\sqrt{26}$ $\displaystyle \sqrt{26}$

$2\sqrt{26}$ $\displaystyle 2\sqrt{26}$

126 $\displaystyle 126$

104 $\displaystyle 104$

Correct answer:

$2\sqrt{26}$ $\displaystyle 2\sqrt{26}$

Explanation:

Use the distance formula to find the length of this line segment:

$\text{Distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle \text{Distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Substitute in the values provided:

$\text{Distance}=\sqrt{(-2-8)^2+(1-(-1))^2}=\sqrt{100+4}=\sqrt{104}$ $\displaystyle \text{Distance}=\sqrt{(-2-8)^2+(1-(-1))^2}=\sqrt{100+4}=\sqrt{104}$

At this point, break down the square root:

$\sqrt{104}=\sqrt{2\cdot52}=\sqrt{2\cdot2\cdot26}=\sqrt{2\cdot2\cdot2\cdot13}$ $\displaystyle \sqrt{104}=\sqrt{2\cdot52}=\sqrt{2\cdot2\cdot26}=\sqrt{2\cdot2\cdot2\cdot13}$

You can remove two of the twos and put them on the outside of the square root symbol, and multiply the two and the thirteen that remain underneath the square root symbol:

$\sqrt{2\cdot2\cdot2\cdot13}=2\sqrt{2\cdot13}=2\sqrt{26}$ $\displaystyle \sqrt{2\cdot2\cdot2\cdot13}=2\sqrt{2\cdot13}=2\sqrt{26}$

Report an Error

Example Question #1 : How To Find The Length Of A Line With Distance Formula

A line segment has endpoints at $(-2, -1)\text{ and }(8, 1)$ $\displaystyle (-2, -1)\text{ and }(8, 1)$. Find the length of this line.

Possible Answers:

$\displaystyle 52$

$2\sqrt{26}$ $\displaystyle 2\sqrt{26}$

$6\sqrt{3}$ $\displaystyle 6\sqrt{3}$

$\displaystyle 96$

Correct answer:

$2\sqrt{26}$ $\displaystyle 2\sqrt{26}$

Explanation:

Use the distance formula to find the length of the line segment.

$D=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$ $\displaystyle D=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

Where,

$\displaystyle (x_1,y_1)=(-2,-1)$ and $\displaystyle (x_2,y_2)=(8,1)$.

$\text{Distance}=\sqrt{(8-(-2))^2+(1-(-1))^2}=\sqrt{100+4}=\sqrt{104}=2\sqrt{26}$ $\displaystyle \text{Distance}=\sqrt{(8-(-2))^2+(1-(-1))^2}=\sqrt{100+4}=\sqrt{104}=2\sqrt{26}$

Report an Error

Example Question #5 : Distance Formula

Find the length of the line segment that has endpoints $(0, 4)\text{ and }(12, 6)$ $\displaystyle (0, 4)\text{ and }(12, 6)$.

Possible Answers:

12.166 $\displaystyle 12.166$

10.659 $\displaystyle 10.659$

12.412 $\displaystyle 12.412$

8.451 $\displaystyle 8.451$

Correct answer:

12.166 $\displaystyle 12.166$

Explanation:

Use the distance formula to find the length of the line segment.

$D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Where,

$\displaystyle (x_1,y_1)=(0,4)$ and $\displaystyle (x_2,y_2)=(12,6)$.

$\text{Distance}=\sqrt{(12-0)^2+(6-4)^2}=\sqrt{144+4}=\sqrt{148}=12.166$ $\displaystyle \text{Distance}=\sqrt{(12-0)^2+(6-4)^2}=\sqrt{144+4}=\sqrt{148}=12.166$

Report an Error

Example Question #6 : Distance Formula

Find the length of the line segment that has the endpoints $(2, 4)\text{ and }(7, 8)$ $\displaystyle (2, 4)\text{ and }(7, 8)$.

Possible Answers:

$\displaystyle 3$

$\sqrt{31}$ $\displaystyle \sqrt{31}$

$\sqrt{29}$ $\displaystyle \sqrt{29}$

$\sqrt{41}$ $\displaystyle \sqrt{41}$

Correct answer:

$\sqrt{41}$ $\displaystyle \sqrt{41}$

Explanation:

Use the distance formula to find the length of the line.

$D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Where,

$\displaystyle (x_1,y_1)=(2,4)$ and $\displaystyle (x_2,y_2)=(7,8)$.

$\text{Distance}=\sqrt{(7-2)^2+(8-4)^2}=\sqrt{25+16}=\sqrt{41}$ $\displaystyle \text{Distance}=\sqrt{(7-2)^2+(8-4)^2}=\sqrt{25+16}=\sqrt{41}$

Report an Error

Example Question #7 : Distance Formula

One leg of a triangle has endpoints at the coordinates $(-1, -2)\text{ and }(-4, -1)$ $\displaystyle (-1, -2)\text{ and }(-4, -1)$. Find the length of this leg.

Possible Answers:

$2\sqrt2$ $\displaystyle 2\sqrt2$

$\displaystyle 8$

$\displaystyle 10$

$\sqrt{10}$ $\displaystyle \sqrt{10}$

Correct answer:

$\sqrt{10}$ $\displaystyle \sqrt{10}$

Explanation:

Use the distance formula to find the length of the leg.

$D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Where,

$\displaystyle (x_1,y_1)=(-1,-2)$ and $\displaystyle (x_2,y_2)=(-4,-1)$.

$\text{Length}=\sqrt{(-4-(-1))^2+(-1-(-2))^2}=\sqrt{9+1}=\sqrt{10}$ $\displaystyle \text{Length}=\sqrt{(-4-(-1))^2+(-1-(-2))^2}=\sqrt{9+1}=\sqrt{10}$

Report an Error

Example Question #101 : Lines

A side of a square is graphed onto a coordinate plane. The side has endpoints at $(-3, 1)\text{ and }(4, -1)$ $\displaystyle (-3, 1)\text{ and }(4, -1)$. Find the length of the side of the square.

Possible Answers:

$\sqrt{53}$ $\displaystyle \sqrt{53}$

$3\sqrt5$ $\displaystyle 3\sqrt5$

$\displaystyle 45$

$\displaystyle 53$

Correct answer:

$\sqrt{53}$ $\displaystyle \sqrt{53}$

Explanation:

Use the distance formula to find the length of the line segment.

$D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Where,

$\displaystyle (x_1,y_1)=(-3,1)$ and $\displaystyle (x_2,y_2)=(4,-1)$

$\text{Distance}=\sqrt{(4-(-3))^2+(-1-1)^2}=\sqrt{49+4}=\sqrt{53}$ $\displaystyle \text{Distance}=\sqrt{(4-(-3))^2+(-1-1)^2}=\sqrt{49+4}=\sqrt{53}$

Report an Error

Example Question #102 : Lines

The side of a triangle is graphed onto a coordinate plane. The side has endpoints at $(2, 2)\text{ and }(1, -5)$ $\displaystyle (2, 2)\text{ and }(1, -5)$. Find the length of this side.

Possible Answers:

$5\sqrt2$ $\displaystyle 5\sqrt2$

$\displaystyle 50$

$4\sqrt{3}$ $\displaystyle 4\sqrt{3}$

$\displaystyle 48$

Correct answer:

$5\sqrt2$ $\displaystyle 5\sqrt2$

Explanation:

Use the distance formula to find the length of the line segment.

$D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Where,

$\displaystyle (x_1,y_1)=(2,2)$ and $\displaystyle (x_2,y_2)=(1, -5)$.

$\text{Distance}=\sqrt{(1-2)^2+(-5-2)^2}=\sqrt{1+49}=\sqrt{50}=5\sqrt2$ $\displaystyle \text{Distance}=\sqrt{(1-2)^2+(-5-2)^2}=\sqrt{1+49}=\sqrt{50}=5\sqrt2$

Report an Error

Example Question #10 : Distance Formula

Find the length of a line segment that has endpoints at $(1, 2)\text{ and }(5, 1)$ $\displaystyle (1, 2)\text{ and }(5, 1)$.

Possible Answers:

$\sqrt{17}$ $\displaystyle \sqrt{17}$

$\sqrt{15}$ $\displaystyle \sqrt{15}$

$\displaystyle 17$

$\displaystyle 15$

Correct answer:

$\sqrt{17}$ $\displaystyle \sqrt{17}$

Explanation:

Use the distance formula to find the length of the line segment.

$D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Where,

$\displaystyle (x_1,y_1)=(1,2)$ and $\displaystyle (x_2,y_2)=(5,1)$

$\text{Distance}=\sqrt{(5-1)^2+(1-2)^2}=\sqrt{16+1}=\sqrt{17}$ $\displaystyle \text{Distance}=\sqrt{(5-1)^2+(1-2)^2}=\sqrt{16+1}=\sqrt{17}$

Report an Error

View SSAT- Upper Level Tutors

Sasha
Certified Tutor

Arizona State University, Bachelor of Science, Biochemistry.

View SSAT- Upper Level Tutors

Wardell
Certified Tutor

SIU Edwardsville, Bachelor in Arts, English.

View SSAT- Upper Level Tutors

Myrtle
Certified Tutor

Southern University and A M College, Bachelor of Education, English. New Mexico State University-Main Campus, Doctor of Educ...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Phoenix, French Tutors in Denver, Statistics Tutors in Seattle, Math Tutors in Denver, GMAT Tutors in Philadelphia, GRE Tutors in San Francisco-Bay Area, Chemistry Tutors in Boston, Chemistry Tutors in Dallas Fort Worth, Reading Tutors in Chicago, LSAT Tutors in Philadelphia

Popular Courses & Classes

MCAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Boston, ACT Courses & Classes in Miami, SAT Courses & Classes in Phoenix, ISEE Courses & Classes in San Diego, ISEE Courses & Classes in Washington DC, GRE Courses & Classes in Los Angeles, SAT Courses & Classes in Houston, ACT Courses & Classes in Phoenix, MCAT Courses & Classes in Chicago

Popular Test Prep

GMAT Test Prep in Boston, ISEE Test Prep in Boston, SSAT Test Prep in Houston, SSAT Test Prep in Philadelphia, LSAT Test Prep in Washington DC, ACT Test Prep in Phoenix, SSAT Test Prep in Washington DC, LSAT Test Prep in San Diego, SAT Test Prep in Boston, ISEE Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Distance Formula

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #91 : Coordinate Geometry

Example Question #92 : Coordinate Geometry

Example Question #371 : Ssat Upper Level Quantitative (Math)

Example Question #1 : How To Find The Length Of A Line With Distance Formula

Example Question #5 : Distance Formula

Example Question #6 : Distance Formula

Example Question #7 : Distance Formula

Example Question #101 : Lines

Example Question #102 : Lines

Example Question #10 : Distance Formula

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: