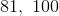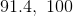The mean is just the average of all the test scores, which is found by adding up the scores and dividing by the number of scores ($\displaystyle 15$).  This gives $\displaystyle 91.4$ as the mean.  The mode is the score which occurs most frequently.  In this case, the mode is $\displaystyle 89$.  The median, the middle score of the sequence, is $\displaystyle 91$.

Let's think of this list of numbers:

2, 4, 6, ...

Where does it end? The first 5 even numbers goes to 10. That means that the last number in the first 20 will be the number 40. So the question is, "Where is the middle?" Well, this is an even number of values, so there is no actual middle. What we have to do, then is find the 10th and the 11th numbers and take their average. The 10th number is easy, based on what we just said. If the 5th is 10, then the 10th is 20. The 11th will just be two more than that, namely 22. To calculate the median, we just have to find the average of those two numbers:

$\displaystyle \frac{20+22}{2}=21$

If you prefer to write out the full list:

2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40

To answer this question, you need to know the first ten prime numbers! Remember, prime numbers are all of the integers that are divisible only by themselves and by 1.  They do not include 1.  So, our list is:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29

The median is the "middle value." There is no proper "middle" since we have an even number of values. We need to take the 5th and the 6th elements (the middle two values) and average them. The 5th term is 11 and the 6th is 13; therefore, the median is:

$\displaystyle \frac{11+13}{2}=\frac{24}{2}=12$

The first thing to do is figure out which stalk is in the "middle." Since there are an even number of stalks, there is no exact middle; there are 500 on one side and 500 on the other. This means that the 500th and the 501st are the median. These will have to be averaged.

Now, we need to determine the height of these two stalks. Consider the pattern given:

1st stalk: 10 feet

2nd stalk: 20 feet

3rd stalk: 30 feet

4th stalk: 40 feet

You should see the pattern that emerges for this problem. Each stalk is 10 times that stalk's place in the row. This means that the 500th stalk will be:

$\displaystyle 500*10 =5000$

The 501st stalk will be:

$\displaystyle 501*10=5010$

The average of these two numbers is:

$\displaystyle \frac{5000+5010}{2} = \frac{10010}{2}=5005$

5005 feet is the median.

The median in a data set is the number that lies directly in the middle. To determine the median, first list the numbers in ascending order:

$\displaystyle 1,4,5,5,6,9,10,11,12,13,16,17,21,28,32,41,50$

Then, count in from both sides to find the number that lies directly in the middle. Therefore the correct answer is "median".

Reorder the numbers in ascending order (from lowest to highest):

11, 13, 13, 13, 13, 14, 16, 19

Find the middle number. In this case, the middle number is the average of the 4th and 5th numbers. Because both the 4th and 5th number are 13, the answer is simply 13.

List the numbers in ascending order: 2,3,4,4,6,8,9,11,13,15,16

The median is the middle number, or 8.

To find the median of a set of values, simply place the numbers in order and find the value that is exactly "in the middle." Here, we can place the test scores in ascending order to get $\displaystyle 61$, $\displaystyle 72$, $\displaystyle 85$, $\displaystyle 85$, $\displaystyle 92$. (Descending order would work just as well.) The median is the middle value, $\displaystyle 85$. Make sure you don't confuse median with mean (average)! To get the mean value of this set, you would find the sum of the test scores and then divide by the number of values.

To find the median, first you arrange the numbers in order from least to greatest.

Then you count how many numbers you have and divide that number by two. In this case 12,15,16,21,22,32,93,108= 8 numbers.

So $\displaystyle \frac{8}{2}=4$

Then starting from the least side of the numbers count 4 numbers till you reach the median number of $\displaystyle 21$

Then starting from the greatest side count 4 numbers until you reach the other median number of $\displaystyle 22$

Finally find the mean of the two numbers by adding them together and dividing them by two $\displaystyle \frac{(21+22)}{2}=\frac{43}{2}$

to find the median number of $\displaystyle 21.5$.

First, arrange all of the data in numerical order: $\displaystyle 3,3,4,4,4,5,5,6,6,7,8$.

Then locate the middle number by using the formula

 $\displaystyle \frac{n-1}{2}+1$, which gives you the location of the median in the ordered data set and where $\displaystyle n$ is the number of terms in the data set.

Here, there are 11 terms.

So, $\displaystyle \frac{11-1}{2}+1=\frac{10}{2}+1=5+1=6.$ 

Therefore, our number is the $\displaystyle 6^{th}$ one in the list, which is $\displaystyle 5$.