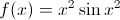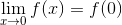All AP Calculus AB Resources
Example Questions
Example Question #1 : Functions, Graphs, And Limits










Example Question #2 : Geometric Understanding Of Graphs Of Continuous Functions

Consider the graph of above. What can we say about
when

Two or more of these are correct.





None of these are correct.


Note that 


The other two are incorrect because sharp turns only apply when we want to take the derivative of something. The derivative of a function at a sharp turn is undefined, meaning the graph of the derivative will be discontinuous at the sharp turn. (To see why, ask yourself if the slope at 
In this case, to get from 

Example Question #24 : Functions, Graphs, And Limits
Is the following piecewise function continuous for all 
No. The function is not continuous at both 

No. The function is not continuous at 
No. There are sharp turns at 

Yes. The function is continuous at all 
No. The function is not continuous at 
Yes. The function is continuous at all 
To check if the piecewise function is continuous, all we need to do is check that the values at 3 and 5 line up.
At 



Plugging 3 into both, we see that both of them are 12 at 
Next, for 


As all three equations are polynomials, we know they will be continuous everywhere else, and they meet up smoothly at the piecewise bounds, thus ensuring that the function is continuous everywhere.
Note, there are sharp turns at 

Example Question #21 : Functions, Graphs, And Limits
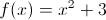


At 
both continuous and diffentiable
neither differentiable or continuous
undefined
continuous but not differentiable
differentiable but not continuous
both continuous and diffentiable
The answer is both.
If graphed the student will see that the two graphs are continuous at 
Example Question #22 : Functions, Graphs, And Limits
Which of the following functions contains a removeable discontinuity?
A removeable discontinuity occurs whenever there is a hole in a graph that could be fixed (or "removed") by filling in a single point. Put another way, if there is a removeable discontinuity at 



For example, the function 




Thus, we could say that 
As we can see, the limit of 


What this means is that 




The functions

have discontinuities, but these discontinuities occur as vertical asymptotes, not holes, and thus are not considered removeable.
The functions



The answer is

Example Question #2 : Continunity As A Property Of Functions
If 
We cannot conclude any of the other answers.






We cannot conclude any of the other answers.
Unless we are explicitly told so, via graph, information, or otherwise, we cannot assume 




We cannot assume anything about the existence of 

Example Question #1 : Understanding Continuity In Terms Of Limits
Which of the following is equal to 


The limit of a function as 




Example Question #2 : Understanding Continuity In Terms Of Limits
Determine any points of discontinuity for the function:
For a function to be continuous the following criteria must be met:
- The function must exist at the point (no division by zero, asymptotic behavior, negative logs, or negative radicals).
- The limit must exist.
- The point must equal the limit. (Symbolically,
).
It is easiest to first find any points where the function is undefined. Since our function involves a fraction and a natural log, we must find all points in the domain such that the natural log is less than or equal to zero, or points where the denominator is equal to zero.
To find the values that cause the natural log to be negative we set
Therefore, those x values will yield our points of discontinuity. Normally, we would find values where the natural log is negative; however, for all 
All AP Calculus AB Resources