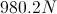The free body diagram of the system is shown below:

Notice how the friction is pointing downward. This is because it is fighting against the applied upward force. If there were no applied upward force, the force of friction would be pointing upward.

The moment before the block begins to move upward, all vertical forces sum to equal 0. Therefore, we can write:

$\displaystyle F - f - mg = 0$

$\displaystyle F = f+mg$

$\displaystyle f$is the force of friction, and $\displaystyle mg$ is the weight of the block

We know that the force of friction can be written as a function of the normal force and coefficient of friction:

$\displaystyle f = \mu_s N$

Substituting, we get:

$\displaystyle F = \mu_s N + mg$

We know all the variables on the right, so we can plug in and solve:

$\displaystyle F = (0.15 \cdot 10) + (1 \cdot 10) = 11.5 N$

You need to have a firm understanding of static friction in order to answer this question correctly.

The main concept covered in this question is that static fricton between two objects has a max and a min, and can have any value between the max and min.

The max static frictional force can be calculated by the equation:

$\displaystyle F_s = \mu_s N$

where mu is the coefficient of friction and N is the normal force

In this problem we get:

$\displaystyle F_s = 0.25(20kg\cdot10\frac{m}{s^2}) = 50N$

However, this is not the answer. The problem statement says that the man is pushing with a force of 35N. Since this is less than the max force calculated, the box will not move. Therefore, the force applied from friction is equal to the force applied by the man, 35N. If these forces were not balanced, then there would be a net force in the opposite direction of the man pushing and the box would accelerate due to friction; this is not possible.

We can use the equation for conservation of energy to solve this problem:

$\displaystyle E = U_i+K_i=U_f+K_f+F$

Plugging in our expressions and canceling initial kinetic and final potential energy, we get:

$\displaystyle mgh_i = \frac{1}{2}mv_f^2 + \mu_kF_Nd$

Rearranging for the coeffeicient of friction:

$\displaystyle \mu_k = \frac{mgh_i - \frac{1}{2}mv_f^2}{F_Nd}$

We now need to determine expressions for the normal force and the distance the sledder travels:

Normal force:

$\displaystyle F_N = mcos(\theta)$

Distance of slope:

$\displaystyle h = dsin(\theta)\rightarrow d=\frac{h}{sin(\theta)}$

Plugging these into the expression for the coefficient of friction, we get:

$\displaystyle \mu_k = \frac{mgh_i - \frac{1}{2}mv_f^2}{\frac{mcos(\theta)h}{sin(\theta)}} = \frac{gh_i - \frac{1}{2}v_f^2}{hcot(\theta)}$

We know all of our variables, allowing us to solve:

$\displaystyle \mu_k = \frac{(10\frac{m}{s^2})(25m)-\frac{1}{2}(20\frac{m}{s})^2}{(25m)cot(30^{\circ})}$

$\displaystyle \mu_k =1.15$ 

Work is equal to the change in energy of the system. We are given the weight of the box and the vertical displacement, which will allow us to calculate the change in potential energy. This will be the total work required to move the box against gravity.

$\displaystyle W_g=\Delta PE=mg\Delta h$

$\displaystyle W_g=(50N)(4m)=200J$

The remaining work that the man exerts must have been used to counter the force of friction acting against his motion.

$\displaystyle W_{total}=W_g+W_f$

$\displaystyle W_f=270J-200J=70J$

Now we know the work performed by friction. Using this value, we can work to solve for the force of friction and the coefficient of friction. First, we will need to use a second formula for work:

$\displaystyle W=Fd$

In this case, the distance will be the distance traveled along the surface of the incline. We can solve for this distance using trigonometry.

$\displaystyle \sin(\theta)=\frac{opp}{hyp}$

$\displaystyle \sin(30^o)=\frac{4m}{d}=$

$\displaystyle d=\frac{4m}{\frac{1}{2}}=8m$

We know the work done by friction and the distance traveled along the incline, allowing us to solve for the force of friction.

$\displaystyle W_f=F_f*d$

$\displaystyle 70J=F_f(8m)$

$\displaystyle F_f=\frac{70J}{8m}=8.75N$

Finally, use the formula for frictional force to solve for the coefficient of friction. Keep in mind that the force on the box due to gravity will be equal to $\displaystyle mg\cos(\theta)$.

$\displaystyle F_f=\mu F_N=\mu(-F_g)$

$\displaystyle F_g=mg\cos(\theta)$

$\displaystyle F_f=\mu(-mg\cos(\theta))$

Plug in our final values and solve for the coefficient of friction.

$\displaystyle 8.75N=-\mu(-50N)\cos(30^o)=\mu(50N)(0.866)$

$\displaystyle \mu=\frac{8.75N}{50N(0.866)}=0.20$

In order for the crate to not slide, the truck has to exert a frictional force on it. The force of friction is related to the normal force by the coefficient of friction.

$\displaystyle F_N=mg$

$\displaystyle F_{friction}=\mu_sF_N=\mu_smg$

This frictional force comes from the acceleration of the truck, based on Newton's second law.

$\displaystyle F_T=ma_T$

The two forces will be equal when the truck is at maximum acceleration without the crate moving.

$\displaystyle F_T=F_f$

$\displaystyle ma=\mu_smg$

Solve for the acceleration.

$\displaystyle a=\mu_sg$

$\displaystyle a=(0.4)(9.8\frac{m}{s^2})$

$\displaystyle a=3.92\frac{m}{s^2}$

We can use the equation for conservation of energy to solve this problem.

$\displaystyle E = U_i+K_i = U_f+K_f+W$

The work in this scenario is done by friction. The only term we can remove from this equaiton is final potential energy. Substituting expressions for each term, we get:

$\displaystyle mgh_i+\frac{1}{2}mv_i^2=\frac{1}{2}mv_f^2+\mu_k F_N d$

We need to determine initial height and the normal force of the skier before we can solve for the coefficient of friction.

$\displaystyle h_i = dsin(30^{\circ})$

$\displaystyle F_N = mgcos(30^{\circ})$

Substitute these into the original equation:

$\displaystyle mgdsin(30^{\circ})+\frac{1}{2}mv_i^2=\frac{1}{2}mv_f^2+\mu_k mgdcos(30^\circ)$

Canceling out mass and rearranging for the coefficient of friction, we get:

$\displaystyle \mu_k = \frac{2gdsin(30^{\circ})+v_i^2-v_f^2}{2gdcos(30^{\circ})}$

Plug in our given values to solve:

$\displaystyle \mu_k = \frac{2(10\frac{m}{s^2})(100m)sin(30^{\circ})+(10\frac{m}{s})^2-(30\frac{m}{s})^2}{2(10\frac{m}{s^2})(100m)cos(30^{\circ})}$

$\displaystyle \mu_k = 0.12$

The maximum force that can be applied will be equal to the maximum value of the static friction force. The formula for friction is:

$\displaystyle F_{friction}=\mu*F_{Normal}$

We also know that the normal force is equal and opposite the force of gravity.

$\displaystyle F_{Normal}=-(F_g)=-mg$

Substituting to the original equation, we can rewrite the force of friction.

$\displaystyle F_{Friction}=\mu*-(mg)$

Using the given values for the coefficient of friction and mass, we can calculate the force using the acceleration of gravity.

$\displaystyle F_{friction}=0.4*-(40 kg*-9.8\frac{m}{s^2})= 156.8 N$
 

We first draw a force diagram:

Note that since the box is originally moving with a velocity of $\displaystyle 5\frac{m}{s}$, it is moving to the right since its velocity is positive. This implies that friction, which always opposes motion, is directed to the left as shown in the diagram. From our diagram we have the following equations:

$\displaystyle N-mg=0$ and $\displaystyle -f=ma$

To know how much time it will take for the box to stop, we need to know the acceleration of the box. Note that the acceleration is constant since friction is a constant force acting on the box. We can fin friction using the following equation:

$\displaystyle f=\mu*N$, where $\displaystyle \mu$ is the coefficient of friction and $\displaystyle N$ the normal force. So we have;

$\displaystyle -f=ma$

$\displaystyle -\mu*N=ma$

$\displaystyle -\mu*mg=ma$

$\displaystyle a=-\mu*g$

Now that we know our acceleration, we can figure out how much time it will take the box to come to a box with the following equation:

$\displaystyle a=\frac{V_f-V_i}{t}$

Where the final velocity is $\displaystyle 0\frac{m}{s}$ since the box comes to a stop.

$\displaystyle -\mu*g=\frac{0\frac{m}{s} -V_i}{t}=-\frac{-V_i}{t}$

$\displaystyle t=\frac{-V_i}{-\mu *g}=\frac{-5\frac{m}{s}}{-(0.1)*(9.8\frac{m}{s^2})}=5.1 s$

Note that there is no such thing as negative time, so you should be able to dismiss those answer choices right away. You must be very careful with using the correct signs for every vector.

Recall the formula to determine kinetic friction:

$\displaystyle F_{kinetic}=\mu N$

Here, $\displaystyle F_{kinetic}$ is the kinetic friction force, $\displaystyle \mu$ is the constant of friction, and $\displaystyle N$ is the magnitude of the normal force of the object in question. Recall that the formula for the normal force is given by:

$\displaystyle F_{normal}=mgcos(\theta)$

Here, $\displaystyle m$ is the mass of the object, $\displaystyle g$ is the gravitational constant, and $\displaystyle \theta$ is the angle of elevation. Since the object is lying $\displaystyle 60^o$ to the horizontal, the normal force it feels is:

$\displaystyle F_{normal}=4.5kg*10\frac{m}{s^2}*cos(60^o)= 4.5kg*10\frac{m}{s^2}*\frac{1}{2}$

$\displaystyle F_{normal}=22.5N$

Therefore,

$\displaystyle F_{kinetic}=0.3*22.5= 7.5N$

To solve for the units, we simply have to solve for $\displaystyle \mu$ and determine its units. 

$\displaystyle \mu=\frac{F_{friction}}{F_{normal}}$

Both friction and normal forces have units of newtons $\displaystyle N$, which means that $\displaystyle \mu$ has units $\displaystyle \frac{F}{F}=1$. 

Therefore, $\displaystyle \mu$ is a dimensionless term and has no units.