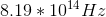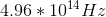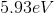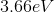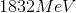Using

\(\displaystyle c=\lambda*\nu\)

Converting \(\displaystyle nm\) to \(\displaystyle m\) and plugging in values

\(\displaystyle 3.00*10^8=605*10^{-9}*\nu\)

\(\displaystyle \nu=4.96*10^{14}Hz\)

Using

\(\displaystyle E=\frac{hc}{\lambda}\)

\(\displaystyle E\) is the photon energy

\(\displaystyle h\) is Plank's constant, \(\displaystyle 6.626*10^{-34}J*s\)

\(\displaystyle c\) is the speed of light, \(\displaystyle 3.00*10^8\frac{m}{s}\)

\(\displaystyle \lambda\) is the wavelength

Converting \(\displaystyle nm\) to \(\displaystyle m\) and plugging in values:

\(\displaystyle E=\frac{6.626*10^{-34}*3.00*10^{8}}{605*10^{-9}}\)

\(\displaystyle E=3.29*10^{-19}J\)

The wavelength of the light beam doesn't depend on the speed through the medium. As such, as can solve for wavelength \(\displaystyle \lambda\) by simply solving:

\(\displaystyle \lambda f=c\)

Where \(\displaystyle f\) is frequency and \(\displaystyle c\) is the speed of light in a vacuum. 

\(\displaystyle \lambda=\frac{c}{f}=\frac{3*10^8 \frac{m}{s}}{100\frac{1}{s}}=3*10^6m\)

To determine the work function of the metal, we can begin by calculating the kinetic energy of the electron from its speed.

\(\displaystyle K=\frac{1}{2}mv^{2}=\frac{1}{2}\left ( 9.1\cdot 10^{-31}kg\right )\left ( 8.6\cdot 10^{5}\frac{m}{s}\right )^{2}=3.36\cdot 10^{-19}J\)

Then, convert joules into electron volts:

\(\displaystyle K=3.36\cdot 10^{-19}J\left ( \frac{1ev}{1.6\cdot 10^{-19}\: J} \right )=2.1eV\)

Next, we'll calculate the energy of the light by using its frequency according to the equation:

\(\displaystyle E=hf=\left ( 6.63\cdot 10^{-34}J\cdot s\right )\left ( 3.76\cdot 10^{14}sec^{-1}\right )=2.49\cdot 10^{-19}J\)

Then, we can convert this energy into electron volts:

\(\displaystyle 2.49\cdot 10^{-19}J\left ( \frac{1eV}{1.6\cdot 10^{-19}J} \right )=1.56eV\)

And finally, we can use the equation for work function:

\(\displaystyle K=\phi -hf\)

\(\displaystyle \phi=K+hf=2.10eV+1.56eV=3.66eV\)

The energy difference between the second excited state \(\displaystyle E_{3}\) and the ground state \(\displaystyle E_{1}\) will be equal to the photon energy since energy is conserved.

\(\displaystyle \Delta E=E_{3}-E_{1}=hf=\frac{h c}{\lambda}\)

\(\displaystyle \lambda=\frac{hc}{\Delta E}\)

Since the energy difference is in electron volts, they need to be converted to Joules. Another convenient formula is to notice that since \(\displaystyle h\) and \(\displaystyle c\) are constants, they can be converted to electron volts and you can use

\(\displaystyle \lambda=\frac{1240eV}{\Delta E}\)

The ejection of electrons from a metal is known as the photoelectric effect. In fact, it was a key discovery that led to the acceptance of the particle nature of light, because the wave nature of light could not account for this finding.

The key that allowed scientists to find this out was that the speed of electrons ejected from the metal was dependent on the color of the light. The intensity of light had no effect on the speed at which electrons were ejected.

As a part of developing this theory, scientists referred to individual discrete particles of light as photons. In order to eject electrons from the metal, individual photons needed to have a sufficient amount of energy. The intensity of light (with a greater amplitude of its waves) represents a case in which photons are striking the metal at a greater rate. But, the individual energy of the photons could be too low in such a situation, hence why intensity is not the key property here. Instead, a higher frequency of light allows each individual photon to have greater energy - enough to knock the metal's electrons off. Furthermore, as the frequency of the light increases, the energy of the individual photons increases and the kinetic energy of the ejected electrons increases as well. The expression for the energy of a photon is shown as follows.

\(\displaystyle E=hf\)

This is an example of one of Einstein's greatest ideas: the relation between the mass of an object/particle, and the energy contained by the mass. This is given as

\(\displaystyle E=mc^2\)

In order to calculate the energy in our particle, we must make sure that the mass is in units of \(\displaystyle kg\).

\(\displaystyle 1 \mu g = 1 * 10^{-9} kg\)

Now we can plug in numbers to our equation and solve for energy.

\(\displaystyle E = 1 * 10^{-9}kg \left(3.0 * 10^{8}\frac{m}{s} \right )^2 = 9 * 10^{7}J\)

In this question, we're presented with information concerning the mass of a uranium atom. We're told two values: the mass of a uranium atom as measured, and the predicted mass of a uranium atom. We're then asked to determine the nuclear binding energy for uranium.

In order to solve this question, we have to realize the significance of the discrepancy between the observed and predicted mass of uranium. The predicted mass is calculated by adding up the individual masses of each constituent proton, electron, and neutron. However, the reason why the measured mass is less than the predicted mass is due to energy-mass equivalence. When the constituent protons and neutrons come together to form the nucleus, some of their mass is converted into energy, and it is this energy which holds these constituent nucleons together. Because some of the mass is converted into energy, the observed mass is less than what we would predict.

Now that we understand why there is a discrepancy between observed and predicted mass, we can calculate the nuclear binding energy by using Einstein's famous equation.

\(\displaystyle E=\Delta mc^{2}\)

This equation states that the nuclear binding energy is equal to the difference between observed and predicted mass, multiplied by the speed of light squared. So to solve for energy, we can plug in the values given to us.

\(\displaystyle E=(236.9601 amu-235.0349 amu)(3.0* 10^{8} \frac{m}{s})^{2}\)

\(\displaystyle E=(1.9252 amu* \frac{1.66* 10^{-27\: kg}}{1amu})(9.0* 10^{16}\frac{m^{2}}{s^{2}})\)

\(\displaystyle E=2.876* 10^{-10} J* \frac{6.24* 10^{12} MeV}{1 J}=1794MeV\)

The energy from the two grams of helium can be found using \(\displaystyle E=mc^2\)

\(\displaystyle E=(.002kg)(3*10^8\frac{m}{s})^2\)

\(\displaystyle E=1.8*10^{14}J\)

This energy can then be equated to the man's kinetic energy, which can then be used to find the man's velocity.

\(\displaystyle 1.8*10^{14}J=\frac{mv^2}{2}\)

\(\displaystyle 1.8*10^{14}=\frac{(100)(v^2)}{2}\)

\(\displaystyle v\approx1.90*10^{6}\frac{m}{s}\)

In this question, we're given the mass defect of an atom's nucleus and are asked to find the binding energy for this atom.

To begin with, it's important to understand that when protons and neutrons come to be held together within the nucleus of an atom, there is a tremendously powerful force holding them together. This incredibly large force accounts for the mass defect. In other words, the total mass of the nucleus is smaller than the sum of the individual masses of the protons and neutrons that make up that nucleus, and this is due to the strong force.

Einstein's mass-energy equivalence explains the observable mass defect; the mass lost is converted into an enormous amount of energy according to the following equation.

\(\displaystyle E=mc^{2}\)

But first, we'll need to convert the mass given to us in the question stem into grams.

\(\displaystyle 0.520\:amu\cdot \frac{1.66\cdot 10^{-27}\:kg}{1\:amu}=8.6\cdot10^{-28}\:kg\)

Furthermore, because we know the value for the speed of light, we can use this information to solve for the binding energy.

\(\displaystyle E=(8.6\cdot 10^{-28}\:kg)(3.0\cdot 10^{8}\:\frac{m}{s})^{2}\)

\(\displaystyle E=7.74\cdot10^{-11}\:J\)