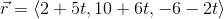Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 3 : Equations of Lines and Planes

Study concepts, example questions & explanations for Calculus 3

Create An Account

All Calculus 3 Resources

6 Diagnostic Tests 373 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Equations Of Lines And Planes

Write down the equation of the line in vector form that passes through the points (2, 10 , -6) , and (-3, 4, 14) .

Possible Answers:

$\vec{r}=\left \langle 2+5t, 10+6t, -6-20t\right \rangle$

$\vec{r}=\left \langle 2+5t, 10-6t, -6-20t\right \rangle$

$\vec{r}=\left \langle 2+5t, 10+6t, -6-2t\right \rangle$

$\vec{r}=\left \langle 2+5t, 1+t, -6-20t\right \rangle$

$\vec{r}=\left \langle 2-5t, 10+6t, -6-20t\right \rangle$

Correct answer:

$\vec{r}=\left \langle 2+5t, 10+6t, -6-20t\right \rangle$

Explanation:

Remember the general equation of a line in vector form:

$\vec{r}=r_0+t\vec{v}=\left \langle x_0,y_0,z_0\right \rangle+t\left \langle a,b,c\right \rangle$ , where $\left \langle x_0,y_0,z_0\right \rangle$ is the starting point, and $\left \langle a,b,c\right \rangle$ is the difference between the start and ending points.

Lets apply this to our problem.

$\vec{r}=\left \langle 2, 10, -6\right \rangle+t\left \langle 5, 6, -20\right \rangle$

Distribute the

$\vec{r}=\left \langle 2, 10, -6\right \rangle+\left \langle 5t, 6t, -20t\right \rangle$

Now we simply do vector addition to get

$\vec{r}=\left \langle 2+5t, 10+6t, -6-20t\right \rangle$

Report an Error

Example Question #111 : Calculus 3

Find the approximate angle between the planes 4x-3y-2z=1 , and 12x+2y-7z=16 .

Possible Answers:

82.1

32.712

None of the other answers.

42.192

52.388

Correct answer:

42.192

Explanation:

Finding the angle between two planes requires us to find the angle between their normal vectors.

To obtain normal vectors, we simply take the coefficients in front of x,y,z .

$\mathbf{n_1} = <4,-3,-2>$

$\mathbf{n_2} = <12,2,-7>$

The (acute) angle between any two vector is

$\theta = \cos^{-1}(\frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\|\|\mathbf{b}\|})$ ,

Substituting, we have

$\theta = \cos^{-1}(\frac{<4,-3,-2> \cdot <12,2,-7>}{\sqrt{16+9+4}\sqrt{144+4+49}})$

$\theta \approx \cos^{-1}(\frac{56}{75.584})$

$\theta \approx 42.192$ .

Report an Error

Example Question #1 : Equations Of Lines And Planes

Find the point of intersection of the plane 2x+y+z=9 and the line described by <2t+4,t-1,-t>

Possible Answers:

The line and the plane are parallel.

$(-\frac{1}{2},5,\frac{1}{2})$

$(0,0,\frac{1}{2})$

(-1,2,-1)

$(5,-\frac{1}{2}, -\frac{1}{2})$

Correct answer:

$(5,-\frac{1}{2}, -\frac{1}{2})$

Explanation:

Substituting the components of the line into those of the plane, we have

2(2t+4)+(t-1)+(-t)=9

4t+8+t-1-t=9

$t = \frac{1}{2}$

Substituting this value of back into the components of the line gives us

$(5,-\frac{1}{2},-\frac{1}{2})$ .

Report an Error

Example Question #1 : Equations Of Lines And Planes

Find the angle (in degrees) between the planes x+y+z =2 , x+y+z = 0

Possible Answers:

42.667

47.333

Correct answer:

Explanation:

A quick way to notice the answer is is to notice the planes are parallel (They only differ by the constant on the right side).

Typically though, to find the angle between two planes, we find the angle between their normal vectors.

A vector normal to the first plane is $\mathbf{n}_1 = <1,1,1>$

A vector normal to the second plane is $\mathbf{n}_2 = <1,1,1>$

Then using the formula for the angle between vectors, $\theta = \cos^{-1} (\frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\| \|\mathbf{b}\|})$ , we have

$\theta = \cos^{-1} (\frac{<1,1,1> \cdot <1,1,1>}{\sqrt{1^2+1^2+1^2} \sqrt{1^2+1^2+1^2}}) = \cos^{-1}(1) = 0$ .

Report an Error

Example Question #2 : Equations Of Lines And Planes

Determine the equation of the plane that contains the following points.

O=(0,0,0)

P=(5,4,0)

Q=(-3,-7,0)

Possible Answers:

y=0

x=0

z=0

5x-7y+z=4

Correct answer:

z=0

Explanation:

The equation of a plane is defined as

$n\bullet<x-x_0,y-y_0,z-z_0>=0$

where is the normal vector of the plane.

To find the normal vector, we first get two vectors on the plane

OP=<5,4,0> and OQ=<-3,-7,0>

and find their cross product.

The cross product is defined as the determinant of the matrix

$\begin{vmatrix} i&j &k \\ 5&4 &0 \\ -3&-7 &0 \end{vmatrix}$

Which is

$=det(\begin{vmatrix} 4&0 \\ -7&0 \end{vmatrix})i-det(\begin{vmatrix} 5&0 \\ -3&0 \end{vmatrix})j+det(\begin{vmatrix} 5&4 \\ -3&-7 \end{vmatrix})k$

=(4*0-(-7)*0)i-(5*0-(-3)*0)j+(5*(-7)-(-3)*4)k

=-23k

Which tells us the normal vector is

<0,0,-23>

Using the point and the normal vector to find the equation of the plane yields

$<0,0,-23>\bullet <x-0,y-0,z-0>=0$

$<0,0,-23>\bullet <x,y,z>=0$

0x+0y+(-23)z=0

Simplified gives the equation of the plane

z=0

Report an Error

Example Question #1 : 3 Dimensional Space

Find the equation of the plane containing the points

O=(0,0,0) P=(0,1,5) Q=(0,-2,-4)

Possible Answers:

x=0

y-4z=1

z=5

y=0

Correct answer:

x=0

Explanation:

The equation of a plane is defined as

$n\bullet<x-x_0,y-y_0,z-z_0>=0$

where is the normal vector of the plane.

To find the normal vector, we first get two vectors on the plane

OP=<0,1,5> and OQ=<0,-2,-4>

and find their cross product.

The cross product is defined as the determinant of the matrix

$\begin{vmatrix} i&j &k \\ 0&1 &5 \\ 0&-2 &-4 \end{vmatrix}$

Which is

$=det(\begin{vmatrix}1&5 \\ -2&-4 \end{vmatrix})i-det(\begin{vmatrix} 0&5 \\ 0&-4 \end{vmatrix})j+det(\begin{vmatrix} 0&1 \\ 0&-2 \end{vmatrix})k$

=(1*(-4)-(-2)*5)i-(0*(-4)-(0)*5)j+(0*(-2)-0*1)k

=6i

Which tells us the normal vector is

<6,0,0>

Using the point and the normal vector to find the equation of the plane yields

$<6,0,0>\bullet <x-0,y-0,z-0>=0$

$<6,0,0>\bullet <x,y,z>=0$

6x+0y+0z=0

Simplified gives the equation of the plane

x=0

Report an Error

Example Question #3 : Equations Of Lines And Planes

Which of the following is an equation of a plane parallel to the plane x+4y-3z=10 ?

Possible Answers:

x+4y-6z=5

2x+4y-3z =5

None of the other answers

x+4y-3z =5

x+8y-3z=5

Correct answer:

x+4y-3z =5

Explanation:

Planes that are parallel to each other only differ (if at all) by the constant on the right-hand side (when both sides are simplified). Since x+4y-3z =5 has the same x,y,z coefficients as the given plane, they are parallel to each other.

Report an Error

Example Question #2 : 3 Dimensional Space

Find a parametric representation of the curve of intersection of the cylinder 9x^2+y^2=9 and the plane x+y+z=7 .

Possible Answers:

$\vec{r}(t)= \left< \cos t, 3 \sin t, 7-\cos t - 3 \sin t\right>$

$\vec{r}(t)= \left< \cos t, 9 \sin t, 7-\cos t - 9 \sin t\right>$

$\vec{r}(t)= \left< \cos t, 3 \sin 3t, 7-\cos t - 3 \sin 3t\right>$

$\vec{r}(t)= \left< \cos t, \sin t, 7-\cos t - \sin t\right>$

Correct answer:

$\vec{r}(t)= \left< \cos t, 3 \sin t, 7-\cos t - 3 \sin t\right>$

Explanation:

We can begin by rewriting the expression for the cylinder as follows

$9x^2 + y^2 = 9 \Rightarrow x^2 + \left( \frac{y}{3} \right) ^2 = 1$ .

This tells us that $x = \cos t, y = 3 \sin t$ . Plugging this back into the equation for the plane x + y + z = 7 to find $z = 7 - x - y = 7 - \cos t - 3 \sin t$ .

This gives us the representation of the curve of intersection as

$\vec{r}(t)= \left< \cos t, 3 \sin t, 7-\cos t - 3 \sin t\right>$ .

Report an Error

Example Question #1 : Equations Of Lines And Planes

Find the equation of the plane containing the following points

O=(2,3,4)

P=(1,5,3)

Q=(5,2,1)

Possible Answers:

x+5y+3z=0

5x-6y+7z=20

2x-2y+z=0

5x-3y+z=4

Correct answer:

5x-6y+7z=20

Explanation:

The equation of a plane is defined as

$n\bullet<x-x_0,y-y_0,z-z_0>=0$

where

is the normal vector of the plane.

To find the normal vector, we first get two vectors on the plane

OP=<1-2,5-3,3-4>=<-1,-2,-1>

and

OQ=<5-2,2-3,1-4>=<3,-1,-3>

and find their cross product.

The cross product is defined as the determinant of the matrix

$\begin{vmatrix} i&j &k \\ -1&-2 &-1 \\ 3&-1 &-3 \end{vmatrix}$

Which is

$=det(\begin{vmatrix} -2&-1 \\ -1&-3 \end{vmatrix})i-det(\begin{vmatrix} -1&-1 \\ 3&-3 \end{vmatrix})j+det(\begin{vmatrix} -1&-2 \\ 3&-1 \end{vmatrix})k$

=(-2(-3)-(-1)*(-1))i-(-1(-3)-3(-1))j+(-1(-1)-3(-2))k

=5i-6j+7k

Which tells us the normal vector is

<5,-6,7>

Using the point

O=(2,3,4)

and the normal vector to find the equation of the plane yields

$<5,-6,7>\bullet<x-2,y-3,z-4>=0$

5(x-2)+(-6)(y-3)+7(z-4)=0

5x-10-6y+18+7z-28=0

Simplified gives the equation of the plane

5x-6y+7z=20

Report an Error

Example Question #10 : Equations Of Lines And Planes

Find the angle in degrees between the planes x+5y-z = 0 and x+z =0

Possible Answers:

67.002

None of the other answers

74.207

23.669

14.282

Correct answer:

74.207

Explanation:

To find the angle between the planes, we find the angle between their normal vectors.

We have

$\mathbf{n}_1 = <1,5,-1>$ , for the first plane, and

$\mathbf{n}_2 = <1,0,-1>$ , for the second plane.

The angle between these two vectors is

$\theta = \cos^{-1}(\frac{\mathbf{n}_1 \cdot \mathbf{n}_2}{\|\mathbf{n}_1\|\|\mathbf{n}_2\|})$

$= \cos^{-1}(\frac{<1,5,-1> \cdot <1,0,-1>}{\sqrt{1^2+(-5)^2+(-1)^2}\sqrt{1^2+0^2+(-1)^2}})$

$\approx \cos^{-1}(\frac{2}{7.34847}) \approx 74.207$

Report an Error

View Calculus 3 Tutors

James
Certified Tutor

St. Mary of the Plains College, Bachelors, Mathematics. Baker University, Masters, Business Administration and Management.

View Calculus 3 Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

View Calculus 3 Tutors

Pankaj
Certified Tutor

University of Delhi, Electrical Engineer, Electrical Engineering. Columbia University in the City of New York, Master of Arts...

All Calculus 3 Resources

6 Diagnostic Tests 373 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in New York City, GRE Tutors in Los Angeles, Math Tutors in Dallas Fort Worth, ACT Tutors in Philadelphia, SSAT Tutors in Houston, Physics Tutors in Chicago, Chemistry Tutors in Chicago, SAT Tutors in New York City, English Tutors in San Diego, Computer Science Tutors in Miami

Popular Courses & Classes

ACT Courses & Classes in San Diego, Spanish Courses & Classes in Atlanta, GRE Courses & Classes in New York City, SSAT Courses & Classes in Seattle, GRE Courses & Classes in Los Angeles, Spanish Courses & Classes in San Diego, ACT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Denver, Spanish Courses & Classes in Chicago, Spanish Courses & Classes in Seattle

Popular Test Prep

SSAT Test Prep in Boston, MCAT Test Prep in Phoenix, ACT Test Prep in San Diego, SAT Test Prep in Atlanta, SSAT Test Prep in Los Angeles, GMAT Test Prep in Washington DC, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in San Francisco-Bay Area, MCAT Test Prep in San Diego, GRE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 3 : Equations of Lines and Planes

Study concepts, example questions & explanations for Calculus 3

All Calculus 3 Resources

Example Questions

Example Question #1 : Equations Of Lines And Planes

Example Question #111 : Calculus 3

Example Question #1 : Equations Of Lines And Planes

Example Question #1 : Equations Of Lines And Planes

Example Question #2 : Equations Of Lines And Planes

Example Question #1 : 3 Dimensional Space

Example Question #3 : Equations Of Lines And Planes

Example Question #2 : 3 Dimensional Space

Example Question #1 : Equations Of Lines And Planes

Example Question #10 : Equations Of Lines And Planes

All Calculus 3 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: