We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number \(\displaystyle 131\textup:\)

When we put this together, we add:

\(\displaystyle 100+30+1=131\)

To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole: 

Let's look at this problem:

\(\displaystyle \frac{\begin{array}[b]{r}.45\\ +\ .13\end{array}}{\ \ \ \ }\)

First, we want to represent the \(\displaystyle .45\) with four tenths blocks and five hundredths blocks: 

Next, we want to take away \(\displaystyle .11\), which means taking away one of the tenths and one of the hundredths:

We can see that we now have three tenths blocks and four hundredths blocks, which means our answer is \(\displaystyle .34\)

We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number \(\displaystyle 131\textup:\)

When we put this together, we add:

\(\displaystyle 100+30+1=131\)

To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole: 

Let's look at this problem:

\(\displaystyle \frac{\begin{array}[b]{r}.56\\ -\ .35\end{array}}{\ \ \ \ }\)

First, we want to represent the \(\displaystyle .56\) with five tenths blocks and six hundredths blocks: 

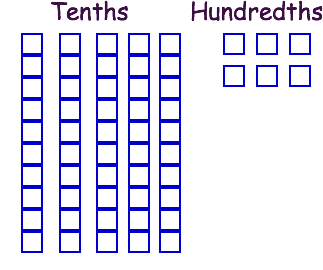
Next, we want to take away \(\displaystyle .35\), which means taking away three of the tenths and five of the hundredths:

We can see that we now have two tenths blocks and one hundredths block, which means our answer is \(\displaystyle .21\)

Subtracting decimals is just like subtracting regular numbers. But, you must remember your decimal in your answer:

\(\displaystyle \frac{\begin{array}[b]{r}.35\\ -\ .13\end{array}}{\ \ \ \ }\)

        \(\displaystyle .22\)

Subtracting decimals is just like subtracting regular numbers. But, you must remember your decimal in your answer:

\(\displaystyle \frac{\begin{array}[b]{r}.83\\ -\ .13\end{array}}{\ \ \ \ }\)

        \(\displaystyle .70\)

Subtracting decimals is just like subtracting regular numbers. But, you must remember your decimal in your answer:

\(\displaystyle \frac{\begin{array}[b]{r}.57\\ -\ .23\end{array}}{\ \ \ \ }\)

        \(\displaystyle .34\)

We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number \(\displaystyle 131\textup:\)

When we put this together, we add:

\(\displaystyle 100+30+1=131\)

To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole: 

Let's look at this problem:

\(\displaystyle \frac{\begin{array}[b]{r}.15\\ -\ .02\end{array}}{\ \ \ \ }\)

First, we want to represent the \(\displaystyle .15\) with one tenths block and five hundredths blocks: 

Next, we want to take away \(\displaystyle .02\), which means taking away none of the tenths and two of the hundredths:

We can see that we now have one tenths block and three hundredths blocks, which means our answer is \(\displaystyle .13\)

Subtracting decimals is just like subtracting whole numbers. But, you must remember your decimal in your answer.

You start subtracting on the far right which in this case is the hundredths place. You cannot take \(\displaystyle 6\) from \(\displaystyle 5\) so we must borrow a tenth from the tenths place. The \(\displaystyle 3\) becomes a \(\displaystyle 2\)  and we carry that tenth into the hundredths place making the \(\displaystyle 5\) a \(\displaystyle 15\).

Next, subtract the tenths place. 

The decimal will be carried down and remain between the tenths place and the ones place. 

The final subtraction portion is the ones place. 

The final answer is \(\displaystyle 2.19\)

Subtracting decimals is just like subtracting whole numbers. But, you must remember your decimal in your answer.

You start subtracting on the far right which in this case is the hundredths place. 

Next, subtract the tenths place 

The decimal will be carried down and remain between the tenths place and the one' place. 

The final subtraction portion is the ones place. 

Subtracting decimals is just like subtracting whole numbers. But, you must remember your decimal in your answer.

You start subtracting on the far right which in this case is the hundredths place. 

Next, subtract the tenths place. 

The decimal will be carried down and remain between the tenths place and the ones place. 

The final subtraction portion is the ones place. 

The final answer is \(\displaystyle 1.65\)

Subtracting decimals is just like subtracting whole numbers. But, you must remember your decimal in your answer.

You start subtracting on the far right which in this case is the hundredths place. 

Next, subtract the tenths place. You cannot take \(\displaystyle 2\) from \(\displaystyle 1\) so we must borrow a one from the ones place. The \(\displaystyle 9\) becomes an \(\displaystyle 8\) and we carry that into the tenths place making the \(\displaystyle 1\) a \(\displaystyle 11\). 

The decimal will be carried down and remain between the tenths place and the ones place. 

The final subtraction portion is the ones place. 

The final answer is \(\displaystyle 4.93\)