All Finite Mathematics Resources
Example Questions
Example Question #1 : Finite Mathematics
A pig's age 

In human years 
To calculate the age of the pig in human years, first recall the equation that given in the question.
Now, identify the known information given in the question.
Since the pig is four years old, the mathematical statement is
Next, substitute in this value into the equation to calculate the human age.
Therefore, the four year old pig is twelve years old in human years.
Example Question #2 : Finite Mathematics
Graph the function.






To graph the function

create an 


Example Question #3 : Finite Mathematics
Which of the following is true of the lines of the equations
and
The lines are parallel.
The lines intersect at one and only one point.
The lines coincide.
The lines are parallel.

To get
in slope-intercept form, add 

The system can thus be stated as
The slope of each line is x-coefficient 
Example Question #2 : Finite Mathematics
What is the total interest made after 4 years on a simple interest loan that accumulates 13% each year and has original amount was $1350.
To solve this problem, first recall the formula to calculate simple interest.
where
From the question it's known that,
Thus the equation becomes,
Therefore $702 in interested accumulated after four years.
Example Question #1 : Mathematics Of Finance
Money is deposited in a bank account at 7% interest per year, compounded bimonthly. If no money is deposited into or withdrawn from the account, then how long will it take for the money to double?
9 years 10 months
10 years 2 months
9 years 6 months
10 years 0 months
9 years 8 months
10 years 0 months
If 



Dividing both sides of the formula by 
The money doubles, so substitute 2 for 




Example Question #3 : Finite Mathematics
Find the value of 

To find the value of 

Now, recall that mod means the remainder after division occurs.
In this case
--------------
Therefore, the remainder is two.
Example Question #4 : Finite Mathematics
The following tables describe matrix operations.

Calculate the following using the tables from above.
This question is testing the matrix operation. Remember to use order of operations and perform the algebraic operation that is inside the parentheses first.
First look at the # table.
Multiplying % by % results in *.
Now go to the $ table and multiply * by %.
Therefore,
Example Question #5 : Finite Mathematics
Find the value of 

To find the value of 

Now, recall that mod means the remainder after division occurs.
In this case
--------------
Therefore, the remainder is three.
Example Question #1 : Finite Mathematics
Give the determinant of 
The determinant of a two-by-two matrix
can be found by evaluating the expression
Substitute the corresponding elements to get

Example Question #1 : Finite Mathematics
Consider the system of linear equations:
What kind of system is this?
Dependent
Consistent and independent
Inconsistent
Consistent and independent
One way to identify whether the matrix is consistent and independent is to form a matrix of its variable coefficients, and calculate its determinant. The matrix is
The determinant of a two-by-two matrix
can be found by evaluating the expression
Substitute the corresponding elements to get
Since 
it follows that the system is consistent and independent.
All Finite Mathematics Resources






















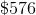


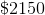

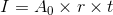



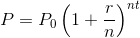


![\ln \left [ \left (1+ \frac{0.07}{6} \right ) ^{6t} \right ]= \ln 2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1033491/gif.latex)