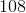GRE Math : Cylinders

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Solid Geometry

The area of the base of a circular right cylinder is quadrupled. By what percentage is the outer face increased by this change?

Possible Answers:

400%

100%

250%

200%

300%

Correct answer:

100%

Explanation:

The base of the original cylinder would have been πr², and the outer face would have been 2πrh, where h is the height of the cylinder.

Let's represent the original area with A, the original radius with r, and the new radius with R: therefore, we know πR² = 4A, or πR² = 4πr². Solving for R, we get R = 2r; therefore, the new outer face of the cylinder will have an area of 2πRh or 2π2rh or 4πrh, which is double the original face area; thus the percentage of increase is 100%. (Don't be tricked into thinking it is 200%. That is not the percentage of increase.)

Report an Error

Example Question #2 : Solid Geometry

What is the surface area of a cylinder with a radius of 17 and a height of 3?

Possible Answers:

2137

2205

2000

3107

1984

Correct answer:

2137

Explanation:

We need the formula for the surface area of a cylinder: SA = 2πr² + 2πrh. This formula has π in it, but the answer choices don't. This means we must approximate π. None of the answers are too close to each other so we could really even use 3 here, but it is safest to use 3.14 as an approximate value of π.

Then SA = 2 * 3.14 * 17² + 2 * 3.14 * 17 * 3 ≈ 2137

Report an Error

Example Question #2 : How To Find The Surface Area Of A Cylinder

What is the surface area of a cylinder with a radius of 6 and a height of 9?

Possible Answers:

64π

225π

180π

108π

96π

Correct answer:

180π

Explanation:

surface area of a cylinder

= 2πr² + 2πrh

= 2π * 6² + 2π * 6 *9

= 180π

Report an Error

Example Question #3 : Solid Geometry

Quantitative Comparison

Quantity A: The volume of a cylinder with a radius of 3 and a height of 4

Quantity B: 3 times the volume of a cone with a radius of 3 and a height of 4

Possible Answers:

Quantity B is greater.

Quantity A is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Correct answer:

The two quantities are equal.

Explanation:

There is no need to do the actual computations here to find the two volumes. The volume of a cone is exactly 1/3 the volume of a cylinder with the same height and radius. That means the two quantities are equal. The formulas show this relationship as well: volume of a cone = πr²h/3 and volume of a cylinder = πr²h.

Report an Error

Example Question #1 : Cylinders

A right circular cylinder of volume $200\pi$ has a height of 8.

Quantity A: 10

Quantity B: The circumference of the base

Possible Answers:

Quantity A is greater

Quantity B is greater

The two quantities are equal

The relationship cannot be determined from the information provided.

Correct answer:

Quantity B is greater

Explanation:

The volume of any solid figure is $base \times height$ . In this case, the volume of the cylinder is $200\pi$ and its height is , which means that the area of its base must be $25\pi$ . Working backwards, you can figure out that the radius of a circle of area $25\pi$ is . The circumference of a circle with a radius of is $10\pi$ , which is greater than .

Report an Error

Example Question #1 : Solid Geometry

What is the surface area of a cylinder that has a diameter of 6 inches and is 4 inches tall?

Possible Answers:

$42\pi$

$10\pi$

$12\pi$

$15\pi$

$4\pi$

Correct answer:

$42\pi$

Explanation:

The formula for the surface area of a cylinder is $\dpi{100} 2\pi r^{2}+ 2\pi rh$ ,

where is the radius and is the height.

$\dpi{100} SA=2\pi (3)^{2}+2\pi (3)(4)$

$\dpi{100} =42\pi$

Report an Error

Example Question #1 : Cylinders

A cylinder has a radius of 4 and a height of 8. What is its surface area?

Possible Answers:

$100\pi$

$128\pi$

$64\pi$

$32\pi$

$96\pi$

Correct answer:

$96\pi$

Explanation:

This problem is simple if we remember the surface area formula!

$SA = 2\pi r^2 +2\pi rh = 2\pi *16+2\pi *4*8 = 32\pi +64\pi = 96\pi$

Report an Error

Example Question #7 : Solid Geometry

Quantitative Comparison

Quantity A: Surface area of a cylinder that is 2 feet high and has a radius of 4 feet

Quantity B: Surface area of a box that is 3 feet wide, 2 feet high, and 4 feet long

Possible Answers:

Quantity A is greater.

Quantity B is greater.

The relationship cannot be determined from the information given.

The two quantities are equal.

Correct answer:

Quantity A is greater.

Explanation:

Quantity A: SA of a cylinder = 2πr² + 2πrh = 2π * 16 + 2π * 4 * 2 = 48π

Quantity B: SA of a rectangular solid = 2ab + 2bc + 2ac = 2 * 3 * 2 + 2 * 2 * 4 + 2 * 3 * 4 = 52

48π is much larger than 52, because π is approximately 3.14.

Report an Error

Example Question #1 : How To Find The Volume Of A Cylinder

A cylinder has a height of 4 and a circumference of 16π. What is its volume

Possible Answers:

64π

256π

16π

128π

none of these

Correct answer:

256π

Explanation:

circumference = πd

d = 2r

volume of cylinder = πr²h

r = 8, h = 4

volume = 256π

Report an Error

Example Question #3 : Solid Geometry

Rusty is considering making a cylindrical grain silo to store his crops. He has an area that is 6 feet long, 6 feet wide and 12 feet tall to build a cylinder in. What is the maximum volume of grain that he can store in this cylinder?

Possible Answers:

$54\pi$

$432\pi$

$108\pi$

108

432

Correct answer:

$108\pi$

Explanation:

The maximum cylindrical base can have a diameter of 6 and therefore a radius of 3. The formula for the volume of a cylinder is 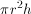$\dpi{100} \small \pi r^{2}h$ , which in this case is $\dpi{100} \small 3\times 3\times 12\times \pi$ .

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Dallas Fort Worth, GMAT Tutors in Denver, Statistics Tutors in Miami, Chemistry Tutors in Atlanta, GMAT Tutors in Philadelphia, GRE Tutors in San Diego, GRE Tutors in Phoenix, Statistics Tutors in Dallas Fort Worth, Biology Tutors in Washington DC, GRE Tutors in Denver

Popular Courses & Classes

Spanish Courses & Classes in New York City, SAT Courses & Classes in Boston, SAT Courses & Classes in Chicago, ISEE Courses & Classes in Los Angeles, SAT Courses & Classes in Denver, ACT Courses & Classes in Los Angeles, LSAT Courses & Classes in San Diego, SSAT Courses & Classes in Chicago, MCAT Courses & Classes in Boston, SAT Courses & Classes in Los Angeles

Popular Test Prep

ISEE Test Prep in Houston, SAT Test Prep in Washington DC, LSAT Test Prep in San Diego, GRE Test Prep in Seattle, LSAT Test Prep in Denver, MCAT Test Prep in New York City, ACT Test Prep in Houston, SAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in New York City, ACT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Cylinders

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : Solid Geometry

Example Question #2 : Solid Geometry

Example Question #2 : How To Find The Surface Area Of A Cylinder

Example Question #3 : Solid Geometry

Example Question #1 : Cylinders

Example Question #1 : Solid Geometry

Example Question #1 : Cylinders

Example Question #7 : Solid Geometry

Example Question #1 : How To Find The Volume Of A Cylinder

Example Question #3 : Solid Geometry

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details