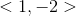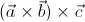Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Vector

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #5 : Parametric, Polar, And Vector

Find the vector where its initial point is (-1,4) and its terminal point is (2,2) .

Possible Answers:

<1,6>

<1,2>

<3,-2>

<1,-2>

Correct answer:

<3,-2>

Explanation:

We need to subtract the -coordinate and the -coordinates to solve for a vector when given its initial and terminal coordinates:

Initial pt: (-1,4)

Terminal pt: (2,2)

Vector: <2-(-1),2-4>

Vector:

Report an Error

Example Question #6 : Parametric, Polar, And Vector

Find the vector where its initial point is (-1,-5) and its terminal point is (2,3) .

Possible Answers:

$\left \langle1,8\right \rangle$

$\left \langle3,2\right \rangle$

$\left \langle3,8\right \rangle$

$\left \langle1,2\right \rangle$

Correct answer:

$\left \langle3,8\right \rangle$

Explanation:

We need to subtract the -coordinate and the -coordinate to solve for a vector when given its initial and terminal coordinates:

Initial pt: (-1,-5)

Terminal pt: (2,3)

Vector: $\left \langle 2-(-1),3-(-5)\right \rangle$

Vector: $\left \langle3,8\right \rangle$

Report an Error

Example Question #1 : Vector

Let $\vec{a}, \vec{b},\vec{c}$ be vectors. All of the following are defined EXCEPT:

Possible Answers:

$(\vec{a}\times \vec{b})\cdot \vec{c}$

$(\vec{a}\cdot \vec{b})\times\vec{c}$

$(\vec{a}\times \vec{b})\cdot(\vec{a}\times \vec{c})$

$(\vec{a}\times \vec{b})\times\vec{c}$

$(\vec{a}\cdot \vec{b})+(\vec{a}\cdot \vec{c})$

Correct answer:

$(\vec{a}\cdot \vec{b})\times\vec{c}$

Explanation:

The cross product of two vectors (represented by "x") requires two vectors and results in another vector. By contrast, the dot product (represented by " $\cdot$ ") between two vectors requires two vectors and results in a scalar, not a vector.

If we were to evaluate $(\vec{a}\cdot \vec{b})\times\vec{c}$ , we would first have to evaluate $\vec{a}\cdot\vec{b}$ , which would result in a scalar, because it is a dot product.

However, once we have a scalar value, we cannot calculate a cross product with another vector, because a cross product requires two vectors. For example, we cannot find the cross product between 4 and the vector <1, 2, 3>; the cross product is only defined for two vectors, not scalars.

The answer is $(\vec{a}\cdot \vec{b})\times\vec{c}$ .

Report an Error

Example Question #8 : Parametric, Polar, And Vector

Find the magnitude of vector v=<3,-2> :

Possible Answers:

$\sqrt{5}$

$\sqrt{13}$

$\sqrt{7}$

$\sqrt{11}$

Correct answer:

$\sqrt{13}$

Explanation:

To solve for the magnitude of a vector, we use the following formula:

$\left \| v \right \|=\sqrt{x^2+y^2}$

v=<3,-2>

$\left \| v \right \|=\sqrt{(3)^2+(-2)^2}$

$\left \| v \right \|=\sqrt{9+}4$

$\left \| v \right \|=\sqrt{13}$

Report an Error

Example Question #9 : Parametric, Polar, And Vector

Given vector u=<0,0> and v=<2,1> , solve for u+v .

Possible Answers:

<2,0>

<2,1>

<0,0>

<0,1>

Correct answer:

<2,1>

Explanation:

u=<0,0> v=<2,1>

To solve for u+v , we need to add the components in the vector and the components together:

u+v=<0+2,0+1>

u+v=<2,1>

Report an Error

Example Question #4 : Vector

Given vector u=<0,0> and v=<2,1> , solve for u-v .

Possible Answers:

<2,1>

<0,-1>

<2,0>

<-2,-1>

Correct answer:

<-2,-1>

Explanation:

u=<0,0> v=<2,1>

To solve for u-v , we need to subtract the components in the vector and the components together:

u-v= <0-2,0-1>

u-v= <-2,-1>

Report an Error

Example Question #3 : Understanding Vector Calculations

Given vector u=<0,0> and v=<2,1> , solve for 2u-3v .

Possible Answers:

<-6,-3>

<2,-3>

<-6,1>

<6,3>

Correct answer:

<-6,-3>

Explanation:

u=<0,0> v=<2,1>

To solve for 2u-3v , We need to first multiply into vector to find and multiply into vector to find ; then we need to subtract the components in the vector and the components together:

2u=<2*0,2*0> = <0,0>

3u=<3*2,3*1> = <6,3>

2u-3v= <0-6,0-3>

2u-3v= <-6,-3>

Report an Error

Example Question #4 : Understanding Vector Calculations

Find the unit vector of v=<5,-12> .

Possible Answers:

$<\frac{5}{13},\frac{-12}{13}>$

$<\frac{-5}{13},\frac{-12}{13}>$

$<\frac{-5}{13},\frac{12}{13}>$

$<\frac{5}{13},\frac{12}{13}>$

Correct answer:

$<\frac{5}{13},\frac{-12}{13}>$

Explanation:

To solve for the unit vector, the following formula must be used:

$\frac{v}{||v||}$

v=<5,-12>

$\left \| v \right \|=\sqrt{(5)^2+(-12)^2}$

$\left \| v \right \|=\sqrt{25+144}$

$\left \| v \right \|=\sqrt{169}$

$\left \| v \right \|=13$

unit vector:

$\frac{<5,-12>}{13}$

$=\frac{1}{13}*<5,-12>$

$=<\frac{5}{13},\frac{-12}{13}>$

Report an Error

Example Question #2 : Understanding Vector Calculations

Is $\langle \frac{5}{13},\frac{-12}{13}\rangle$ a unit vector?

Possible Answers:

no, because magnitude is not equal to

yes, because magnitude is equal to

not enough information given

Correct answer:

yes, because magnitude is equal to

Explanation:

To verify where a vector is a unit vector, we must solve for its magnitude. If the magnitude is equal to 1 then the vector is a unit vector:

$<\frac{5}{13},\frac{-12}{13}>$

$\sqrt{\left(\frac{5}{13}\right)^2+\left(\frac{-12}{13}\right)^2}$

$\sqrt{\left(\frac{25}{169}\right)+\left(\frac{144}{169}\right)$

$\sqrt{\frac{169}{169}}$

$\sqrt{1}$

$<\frac{5}{13},\frac{-12}{13}>$ is a unit vector because magnitude is equal to .

Report an Error

Example Question #3 : Understanding Vector Calculations

Given vector u=<3,3> . Solve for the direction (angle) of the vector:

Possible Answers:

$15^{\circ}$

$90^{\circ}$

$45^{\circ}$

$60^{\circ}$

Correct answer:

$45^{\circ}$

Explanation:

To solve for the direction of a vector, we use the following formula:

$tan\alpha$ = $\frac{b}{a}$

with the vector being $u=\left \langle a,b \right \rangle$

$u=\left \langle 3,3 \right \rangle$

a=3

b=3

$\tan\alpha=\frac{3}{3}=1$

$\alpha = \arctan (1)$

$\alpha =45^{\circ}$

Report an Error

View Tutors

Shivansh
Certified Tutor

University of British Columbia, Bachelor, Math major and data science minor .

View Tutors

Renetta
Certified Tutor

Langston University, Bachelor of Science, Education of Individuals in Elementary Special Education Programs.

View Tutors

Samuel
Certified Tutor

York University, Bachelor, Physics. York University, Master's/Graduate, Mathematics and Statistics.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Seattle, Math Tutors in Atlanta, SAT Tutors in Phoenix, English Tutors in Atlanta, Biology Tutors in Dallas Fort Worth, Algebra Tutors in Phoenix, Reading Tutors in Philadelphia, Reading Tutors in New York City, MCAT Tutors in New York City, Calculus Tutors in Phoenix

Popular Courses & Classes

LSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Miami, SAT Courses & Classes in Denver, MCAT Courses & Classes in Atlanta, GMAT Courses & Classes in Philadelphia, SAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Chicago, LSAT Courses & Classes in Washington DC

Popular Test Prep

GMAT Test Prep in Phoenix, SAT Test Prep in Denver, ACT Test Prep in Atlanta, GMAT Test Prep in Philadelphia, LSAT Test Prep in Boston, LSAT Test Prep in Houston, LSAT Test Prep in Atlanta, MCAT Test Prep in Los Angeles, LSAT Test Prep in Miami, MCAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Vector

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #5 : Parametric, Polar, And Vector

Example Question #6 : Parametric, Polar, And Vector

Example Question #1 : Vector

Example Question #8 : Parametric, Polar, And Vector

Example Question #9 : Parametric, Polar, And Vector

Example Question #4 : Vector

Example Question #3 : Understanding Vector Calculations

Example Question #4 : Understanding Vector Calculations

Example Question #2 : Understanding Vector Calculations

Example Question #3 : Understanding Vector Calculations

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: