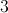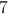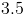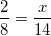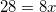We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Quadrilaterals

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Quadrilaterals

What is the area of a kite with diagonals of 5 and 7?

Possible Answers:

17.5

Correct answer:

17.5

Explanation:

To find the area of a kite using diagonals you use the following equation $\frac{a*b}{2}=Area\: of a\: kite$

That diagonals ( and )are the lines created by connecting the two sides opposite of each other.

Plug in the diagonals for and to get $\frac{5*7}{2}=Area$

Then multiply and divide to get the area. $\frac{35}{2}=17.5$

The answer is 17.5

Report an Error

Example Question #2 : Quadrilaterals

Find the area of the following kite:

Kite

Possible Answers:

78m^2

27m^2

54m^2

39m^2

26m^2

Correct answer:

39m^2

Explanation:

The formula for the area of a kite is:

$A = \frac{1}{2}(d_{1}\cdot d_{2})$

Where $d_{1}$ is the length of one diagonal and $d_{2}$ is the length of the other diagonal

Plugging in our values, we get:

$A = \frac{1}{2}(d_{1}\cdot d_{2})$

$A = \frac{1}{2}(6m\cdot 13m) = 39m^2$

Report an Error

Example Question #2 : How To Find The Area Of A Kite

Find the area of the following kite:

Screen_shot_2014-03-01_at_9.16.34_pm

Possible Answers:

$18\sqrt{3}m^2$

$18\sqrt{3}-18m^2$

$18\sqrt{3}+18m^2$

18m^2

20m^2

Correct answer:

$18\sqrt{3}+18m^2$

Explanation:

The formula for the area of a kite is:

$A = \frac{1}{2} (d_1)(d_2)$

where d_1 is the length of one diagonal and d_2 is the length of another diagonal.

Use the formulas for a 45-45-90 triangle and a 30-60-90 triangle to find the lengths of the diagonals. The formula for a triangle is $a-a-a \sqrt{2}$ and the formula for a triangle is $a-a \sqrt{3}-2a$ .

Our 45-45-90 triangle is: $3 \sqrt{2}m-3 \sqrt{2}m-6m$

Our 30-60-90 triangle is: $3 \sqrt{2}m-3 \sqrt{6}m-6\sqrt{2}m$

Plugging in our values, we get:

$A = \frac{1}{2} (d_1)(d_2)$

$A = \frac{1}{2} (6\sqrt{2}m) (3\sqrt{6}m + 3\sqrt{2}m)$

$A = \frac{1}{2} (18\sqrt{12}+18\sqrt{4}) = 18\sqrt{3}+18m^2$

Report an Error

Example Question #1 : How To Find The Perimeter Of Kite

Find the perimeter of the following kite:

Kite

Possible Answers:

$18+\sqrt{10} m$

$10+6\sqrt{10} m$

$16+\sqrt{10} m$

$8+6\sqrt{10} m$

$10+9\sqrt{10} m$

Correct answer:

$10+6\sqrt{10} m$

Explanation:

In order to find the length of the two shorter edges, use a Pythagorean triple:

3-4-5

3m-4m-5m

In order to find the length of the two longer edges, use the Pythagorean theorem:

A^2+B^2=C^2

(9)^2+(3)^2=C^2

C^2=90

$C=3\sqrt{10}m$

The formula of the perimeter of a kite is:

$P = 2(side_{short})+2(side_{long})$

Plugging in our values, we get:

$P = 2(5m)+2(3\sqrt{10}m) = 10+6\sqrt{10}m$

Report an Error

Example Question #1 : How To Find The Perimeter Of Kite

Find the perimeter of the following kite:

Screen_shot_2014-03-01_at_9.16.34_pm

Possible Answers:

$12\sqrt{2}m + 12m$

$12\sqrt{2}m - 12m$

24m

$12\sqrt{3}m - 12m$

$12\sqrt{3}m + 12m$

Correct answer:

$12\sqrt{2}m + 12m$

Explanation:

The formula for the perimeter of a kite is:

$P = 2(s_{long}) + 2(s_{short})$

Where $s_{long}$ is the length of the longer side and $s_{short}$ is the length of the shorter side

Use the formulas for a 45-45-90 triangle and a 30-60-90 triangle to find the lengths of the longer sides. The formula for a triangle is $a-a-a \sqrt{2}$ and the formula for a triangle is $a-a \sqrt{3}-2a$ .

Our 45-45-90 triangle is: $3 \sqrt{2}m-3 \sqrt{2}m-6m$

Our 30-60-90 triangle is: $3 \sqrt{2}m-3 \sqrt{6}m-6\sqrt{2}m$

Plugging in our values, we get:

$P = 2(6\sqrt{2}m) + 2(6m)$

$P = 12\sqrt{2}m + 12m$

Report an Error

Example Question #1 : Trapezoids

The following quadrilaterals are similar. Solve for .

(Figure not drawn to scale).

Possible Answers:

3.5

Correct answer:

3.5

Explanation:

When polygons are similar, the sides will have the same ratio to one another. Set up the appropriate proportions.

$\small \frac{2}{8}=\frac{x}{14}$

Cross multiply.

$\small 28=8x$

$\small x=3.5$

Report an Error

Example Question #1 : How To Find The Area Of A Trapezoid

Find the area of the following trapezoid:

Trapezoid

Possible Answers:

126m^2

252m^2

202m^2

260m^2

180m^2

Correct answer:

252m^2

Explanation:

The formula for the area of a trapezoid is:

$A = \frac{1}{2}(b_{1}+b_{2})(h)$

Where b_1 is the length of one base, b_2 is the length of the other base, and is the height.

To find the height of the trapezoid, use a Pythagorean triple:

5-12-13

5m-12m-13m

Plugging in our values, we get:

$A = \frac{1}{2}(b_{1}+b_{2})(h)$

$A = \frac{1}{2}(16m+26m)(12m)=252m^2$

Report an Error

Example Question #1 : Trapezoids

Find the area of the following trapezoid:

Trapezoid_angles

Possible Answers:

$48+24\sqrt{3}m^2$

$96+12\sqrt{3}m^2$

$54+24\sqrt{6}m^2$

$96+24\sqrt{3}m^2$

$60+24\sqrt{3}m^2$

Correct answer:

$96+24\sqrt{3}m^2$

Explanation:

Use the formula for 30-60-90 triangles in order to find the length of the bottom base and the height.

The formula is:

$a-a\sqrt{3}-2a$

Where is the length of the side opposite the $\measuredangle 30$ .

Beginning with the 12m side, if we were to create a 30-60-90 triangle, the length of the base is $6\sqrt{3}m$ , and the height is .

Creating another 30-60-90 triangle on the left, we find the height is , the length of the base is $2\sqrt{3}m$ , and the side is $4\sqrt{3}m$ .

The formula for the area of a trapezoid is:

$A = \frac{1}{2}(b_{1}+b_{2})(h)$

Where b_1 is the length of one base, b_2 is the length of the other base, and is the height.

Plugging in our values, we get:

$A = \frac{1}{2}(b_{1}+b_{2})(h)$

$A = \frac{1}{2}(16m+16m+6\sqrt{3}m+2\sqrt{3}m)(6m)$

$A = \frac{1}{2}(32m+8\sqrt{3}m)(6m)$

$A = (32m+8\sqrt{3}m)(3m)=96+24\sqrt{3}m^2$

Report an Error

Example Question #2 : Trapezoids

Determine the area of the following trapezoid:

Screen_shot_2014-02-27_at_6.39.24_pm

Possible Answers:

24m^2

28m^2

35m^2

25m^2

20m^2

Correct answer:

24m^2

Explanation:

The formula for the area of a trapezoid is:

$A=\frac{1}{2}(b_{1}+b_{2})(h)$ ,

where b_1 is the length of one base, b_2 is the length of another base, and is the length of the height.

Plugging in our values, we get:

$A=\frac{1}{2}(7m+5m)(4m)=24m^2$

Report an Error

Example Question #1 : How To Find The Area Of A Trapezoid

Find the area of the following trapezoid:

Screen_shot_2014-02-27_at_6.47.22_pm

Possible Answers:

$52\sqrt{91}m^2$

$48\sqrt{101}m^2$

$48\sqrt{81}m^2$

$52\sqrt{101}m^2$

$48\sqrt{91}m^2$

Correct answer:

$48\sqrt{91}m^2$

Explanation:

The formula for the area of a trapezoid is:

$A=\frac{1}{2}(b_{1}+b_{2})(h)$ ,

where b_1 is the length of one base, b_2 is the length of another base, and is the length of the height.

Use the Pythagorean Theorem to find the height of the trapezoid:

A^2+B^2=C^2

6m^2+B^2=20m^2

$B=2\sqrt{91}m$

Plugging in our values, we get:

$A=\frac{1}{2}(18m+30m)(2\sqrt{91}m)=48\sqrt{91}m^2$

Report an Error

View Tutors

Blossom
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Computer Science.

View Tutors

Chukwudi
Certified Tutor

University of Nigeria, Nsukka., Bachelor of Science, Biochemistry. African University of Science and Technology., Master of S...

View Tutors

Jhemson
Certified Tutor

Batangas State University, Doctor of Philosophy, Mathematics.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Miami, GMAT Tutors in Atlanta, Chemistry Tutors in Chicago, Math Tutors in Miami, MCAT Tutors in Chicago, Spanish Tutors in Phoenix, SAT Tutors in Dallas Fort Worth, LSAT Tutors in Chicago, ACT Tutors in Houston, Algebra Tutors in Chicago

Popular Courses & Classes

GRE Courses & Classes in Atlanta, LSAT Courses & Classes in Denver, Spanish Courses & Classes in Denver, Spanish Courses & Classes in Chicago, SAT Courses & Classes in Atlanta, ISEE Courses & Classes in Atlanta, LSAT Courses & Classes in Miami, GMAT Courses & Classes in Washington DC, ISEE Courses & Classes in New York City, ISEE Courses & Classes in Denver

Popular Test Prep

MCAT Test Prep in Boston, SSAT Test Prep in Philadelphia, SAT Test Prep in Boston, SAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Chicago, ACT Test Prep in Denver, GRE Test Prep in Phoenix, MCAT Test Prep in Denver, LSAT Test Prep in San Diego, ACT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Quadrilaterals

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Quadrilaterals

Example Question #2 : Quadrilaterals

Example Question #2 : How To Find The Area Of A Kite

Example Question #1 : How To Find The Perimeter Of Kite

Example Question #1 : How To Find The Perimeter Of Kite

Example Question #1 : Trapezoids

Example Question #1 : How To Find The Area Of A Trapezoid

Example Question #1 : Trapezoids

Example Question #2 : Trapezoids

Example Question #1 : How To Find The Area Of A Trapezoid

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: