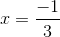Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Understanding Rational Expressions

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Rational Expressions

Solve:

If $\displaystyle y$ varies directly as $\displaystyle x$ , and x=7 $\displaystyle x=7$ when y=21 $\displaystyle y=21$ , find $\displaystyle x$ when y=-5 $\displaystyle y=-5$ .

Possible Answers:

$x=\frac{-7}{3}$ $\displaystyle x=\frac{-7}{3}$

$x=\frac{-11}{3}$ $\displaystyle x=\frac{-11}{3}$

$x=\frac{-13}{3}$ $\displaystyle x=\frac{-13}{3}$

$x=\frac{-1}{3}$ $\displaystyle x=\frac{-1}{3}$

$x=\frac{-5}{3}$ $\displaystyle x=\frac{-5}{3}$

Correct answer:

$x=\frac{-5}{3}$ $\displaystyle x=\frac{-5}{3}$

Explanation:

The formula for a direct variation is:

$\frac{x_1}{x_2}=\frac{y_1}{y_2}$ $\displaystyle \frac{x_1}{x_2}=\frac{y_1}{y_2}$

Plugging in our values, we get:

$\frac{7}{x}=\frac{21}{-5}$ $\displaystyle \frac{7}{x}=\frac{21}{-5}$

21x=-35 $\displaystyle 21x=-35$

$x= \frac{-5}{3}$ $\displaystyle x= \frac{-5}{3}$

Report an Error

Example Question #2 : Rational Expressions

If two boxes have the same depth and capacity, the length is inversely proportional to the width. One box is $60\ cm$ $\displaystyle 60\ cm$ long and $40\ cm$ $\displaystyle 40\ cm$ wide. A second box (same depth and capacity) is $5\ cm$ $\displaystyle 5\ cm$ long. How wide is it?

Possible Answers:

$460\ cm$ $\displaystyle 460\ cm$

$450\ cm$ $\displaystyle 450\ cm$

$470\ cm$ $\displaystyle 470\ cm$

$490\ cm$ $\displaystyle 490\ cm$

$480\ cm$ $\displaystyle 480\ cm$

Correct answer:

$480\ cm$ $\displaystyle 480\ cm$

Explanation:

The formula for an indirect variation is:

$\frac{x_1}{x_2}=\frac{y_2}{y_1}$ $\displaystyle \frac{x_1}{x_2}=\frac{y_2}{y_1}$

Plugging in our values, we get:

$\frac{60\ cm}{5\ cm}=\frac{y}{40\ cm}$ $\displaystyle \frac{60\ cm}{5\ cm}=\frac{y}{40\ cm}$

$5y=2400\ cm$ $\displaystyle 5y=2400\ cm$

$y=480\ cm$ $\displaystyle y=480\ cm$

Report an Error

View Tutors

Erin
Certified Tutor

Messiah College, Bachelor of Science, Health Sciences, General. Messiah College, Master of Science, Occupational Therapy.

View Tutors

Maria Cecilia
Certified Tutor

The University of Texas at El Paso, Bachelor in Arts, Multi-/Interdisciplinary Studies, General. The University of Texas at E...

View Tutors

Charlotte
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, Linguistics. University of North Carolina at Chapel Hill, Mast...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Miami, Biology Tutors in Seattle, Reading Tutors in Denver, SSAT Tutors in Seattle, Physics Tutors in Atlanta, Statistics Tutors in Denver, MCAT Tutors in Phoenix, Math Tutors in New York City, Math Tutors in San Diego, MCAT Tutors in San Diego

Popular Courses & Classes

MCAT Courses & Classes in Boston, GRE Courses & Classes in San Diego, MCAT Courses & Classes in Phoenix, GRE Courses & Classes in Boston, MCAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in New York City, SSAT Courses & Classes in Chicago, Spanish Courses & Classes in Washington DC, SSAT Courses & Classes in Houston, MCAT Courses & Classes in Philadelphia

Popular Test Prep

SSAT Test Prep in New York City, LSAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Philadelphia, SAT Test Prep in Philadelphia, SSAT Test Prep in Atlanta, MCAT Test Prep in Washington DC, ACT Test Prep in Chicago, ISEE Test Prep in Denver, SSAT Test Prep in Houston, GRE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Understanding Rational Expressions

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Rational Expressions

Example Question #2 : Rational Expressions

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: