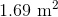When Calvin put up \(\displaystyle \small 32\) feet of molding, he figured out the perimeter of the room was \(\displaystyle \small 32\) feet.  Since he knows that all four walls are the same width, he can use the equation \(\displaystyle \small 4s=P\) to determine the length of each side by plugging \(\displaystyle \small 32\) in for \(\displaystyle \small P\) and solving for \(\displaystyle \small s\).

\(\displaystyle \small 4s=32\)

In order to solve for \(\displaystyle \small s\), Calvin must divide both sides by four.

The left-hand side simplifies to:

\(\displaystyle \small \frac{4s}{4}=s\)

The right-hand side simplifies to:

\(\displaystyle \small \frac{32}{2}=8\)

Now, Calvin knows the width of each room is \(\displaystyle \small 8\) feet.  Next he must find the area of each wall. To do this, he must multiply the width by the height because the area of a rectangle is found using the equation \(\displaystyle \small \small A=l\cdot w\). Since Calvin now knows that the width of each wall is \(\displaystyle \small 8\) feet and that the height of each wall is also \(\displaystyle \small 8\) feet, he can multiply the two together to find the area.

\(\displaystyle \small 8\cdot 8=64\)

Since Calvin wants to find how much paint he needs to cover three walls, he must first find out how many square feet he is covering.  If one wall is \(\displaystyle \small 64\) square feet, he must multiply that by \(\displaystyle \small 3\).

\(\displaystyle \small 64\cdot 3=192\)

Calvin is painting \(\displaystyle \small 192\) square feet. If one can of paint covers 24 square feet, he must divide the total space (\(\displaystyle \small 192\) square feet) by \(\displaystyle \small 24\).

\(\displaystyle \small \frac{192}{24}=8\)

Calvin will need \(\displaystyle \small 8\) cans of paint.

We can actually solve this by comparing volumes; the cube with the greater volume has the greater sidelength and, subsequently, the greater surface area.

The volume of the cube in (b) is the cube of 90 millimeters, or 9 centimeters. This is \(\displaystyle 9 ^{3} = 729 \textrm{ cm}^{3}\), which is greater than \(\displaystyle 512\ cm^{3}\). The cube in (b) has the greater volume, sidelength, and, most importantly, surface area.

A square has four sides of the same length. 

One yard is equal to 36 inches, so each side of the square has length

\(\displaystyle 36 \div 3 = 12\) inches.

Its area is the square of the sidelength, or 

\(\displaystyle 12^{2} = 12 \times 12 = 144\) square inches.

100 centimeters are equal to one meter, so 3,900 centimeters are equal to 

\(\displaystyle 3,900 \div 100 = 39\) meters. 

A square has four sides of the same length. Since the sum of the lengths of three of the congruent sides is 3,900 centimeters, or 39 meters, each side measures

\(\displaystyle 39 \div 3 = 13\) meters.

The area of the square is the square of the sidelength, or

\(\displaystyle 13^{2} =13 \times 13 = 169\) square meters.

The area of a square is the square of its side length:

\(\displaystyle A=s^2\)

Using the side length from the question:

\(\displaystyle A=\left ( 5t\right ) ^{2} = 5 ^{2} \cdot t ^{2} = 25t ^{2}\)

However, it is impossible to tell with certainty which of \(\displaystyle 25t ^{2}\) and \(\displaystyle 25t\) is greater.

For example, if \(\displaystyle t = 2\), 

\(\displaystyle 25t ^{2} = 25 \cdot 2^{2} = 25 \cdot4 = 100\)

and 

\(\displaystyle 25t = 25 \cdot 2 = 50\)

so \(\displaystyle 25t ^{2} > 25t\) if \(\displaystyle t = 2\).

But if \(\displaystyle t = \frac{1}{5}\),

\(\displaystyle 25t ^{2}=25 \cdot \left ( \frac{1}{5} \right )^{2} = 25 \cdot \frac{1}{25} = 1\)

and

\(\displaystyle 25t =25 \cdot \frac{1}{5} = 5\)

so \(\displaystyle 25t ^{2} < 25t\) if \(\displaystyle t = \frac{1}{5}\).

The area formula for a square is length times width. Keep in mind that all of a square's sides are equal.

\(\displaystyle A=l\times w=s\times s\)

So, if one side of a square equals 5, all of the other sides must also equal 5. You will find the area of the square by multiplying two of its sides:

\(\displaystyle s=5\)

\(\displaystyle A=s\times s=5 \times 5 = 25\)

A square plot of land with perimeter one mile has as its sidelength one fourth of this, or \(\displaystyle \frac{1}{4}\) mile; its area is the square of this, or 

\(\displaystyle \frac{1}{4} \times \frac{1}{4} = \frac{1}{16}\) square miles.

One square mile is equivalent to 640 acres, so \(\displaystyle \frac{1}{16}\) square miles is equivalent to 

\(\displaystyle \frac{1}{16} \times 640 = \frac{640}{16} = 40\) acres.

This makes (b) greater.

One kilometer is equal to 1,000 meters, so divide each dimension of the plot in meters by 1,000 to convert to kilometers:

\(\displaystyle 500 \div 1,000= 0.5\) kilometers

\(\displaystyle 200 \div 1,000 = 0.2\) kilometers

Multiply the dimensions to get the area in square kilometers:

\(\displaystyle 0.5 \times 0.2 = 0.1\) square kilometers

Since one square kilometer is equal to 100 hectares, multiply this by 100 to convert to hectares:

\(\displaystyle 0.1 \times 100 = 10\) hectares

This makes (a) the greater.

A square with area 196 square inches has sidelength \(\displaystyle \sqrt{196} = 14\) inches, and therefore has perimeter \(\displaystyle 4 \cdot 14 = 56\) inches

To find the perimeter of a square, you must add together all the sides. In this case, we are adding \(\displaystyle \small \frac{1}{8}\) four times.

\(\displaystyle \small \frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{4}{8}\)

Since all of the denominators are the same, there is no need to find a commond denominator, so we add together the numerators.  This gives us \(\displaystyle \small \frac{4}{8}\).

Since both the numerator and denomator are divisible by four, we must simplify this fraction.

\(\displaystyle \small \frac{4/4}{8/4}= \frac{1}{2}\)

The perimeter of the square is \(\displaystyle \small \small \frac{1}{2}\).