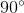All ISEE Upper Level Math Resources
Example Questions
Example Question #1 : Triangles
Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?
An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.
3 feet is equal to 

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Isosceles Triangle
The triangles are similar. Solve for 

Because the triangles are similar, proportions can be used to solve for the length of the side:
Cross-multiply:
Example Question #5 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5
One of the base angles of an isosceles triangle is 
The base angles of an isosceles triangle are always equal. Therefore both base angles are 
Let 
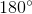
Example Question #1 : Triangles
A right triangle has a hypotenuse of 10 and a side of 6. What is the missing side?
To find the missing side, use the Pythagorean Theorem 



Example Question #2 : Triangles

Refer to the above diagram. Which of the following quadratic equations would yield the value of 
By the Pythagorean Theorem,
Example Question #1 : Right Triangles

Note: Figure NOT drawn to scale.
Refer to the above diagram. Which of the following quadratic equations would yield the value of 
By the Pythagorean Theorem,
Example Question #3 : Triangles

Note: Figure NOT drawn to scale.
Refer to the above diagram.
Find the length of 
First, find 
Since 


Example Question #2 : Right Triangles

Note: Figure NOT drawn to scale.
Refer to the above diagram.
Find the length of 
First, find 
Since 


Example Question #4 : How To Find The Length Of The Side Of A Right Triangle

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 
By the Pythagorean Theorem,
Example Question #3 : Right Triangles
A right triangle 




Insufficient information is given to answer the question.
The arcs intercepted by a right angle are both semicircles, so hypotenuse 


By the Pythagorean Theorem,
All ISEE Upper Level Math Resources