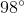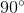Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : Triangles

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Acute / Obtuse Isosceles Triangles

Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?

Possible Answers:

$36 \textrm{ in}$

$54 \textrm{ in}$

$32 \textrm{ in}$

$42 \textrm{ in}$

$40 \textrm{ in}$

Correct answer:

$36 \textrm{ in}$

Explanation:

An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.

3 feet is equal to $3 \times 12 = 36$ inches, and 4 feet is equal to $4 \times 12 = 48$ inches. We choose 36 inches, since that, but not 48 inches, is a choice.

Report an Error

Example Question #2 : Acute / Obtuse Isosceles Triangles

The triangles are similar. Solve for .

Question_12

Possible Answers:

x=2

x=4

x=1

x=3

Correct answer:

x=2

Explanation:

Because the triangles are similar, proportions can be used to solve for the length of the side:

$\frac{9}{3}=\frac{6}{x}$

Cross-multiply:

9x=18

x=2

Report an Error

Example Question #661 : Grade 7

One of the base angles of an isosceles triangle is $42^{\circ}$ . Give the measure of the vertex angle.

Possible Answers:

$86 ^{\circ}$

$98 ^{\circ}$

$96 ^{\circ}$

$90^{\circ}$

$100^{\circ}$

Correct answer:

$96 ^{\circ}$

Explanation:

The base angles of an isosceles triangle are always equal. Therefore both base angles are $42^{\circ}$ .

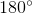
Let the measure of the third angle. Since the sum of the angles of a triangle is $180^{\circ}$ , we can solve accordingly:

$42+42+x=180\Rightarrow x=180-84\Rightarrow x=96^{\circ}$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

A right triangle has a hypotenuse of 10 and a side of 6. What is the missing side?

Possible Answers:

Correct answer:

Explanation:

To find the missing side, use the Pythagorean Theorem (a^2+b^2=c^2) . Plug in (remember c is always the hypotenuse!) so that 6^2+b^2=10^2 . Simplify and you get 36+b^2=100. Subtract 36 from both sides so that you get b^2=64. Take the square root of both sides. B is 8.

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

Right_triangle

Refer to the above diagram. Which of the following quadratic equations would yield the value of as a solution?

Possible Answers:

$2x^{2}+6x-11 = 0$

$x^{2}+6x+409 = 0$

$x^{2}+6x-391 = 0$

$2x^{2}+6x-391 = 0$

$2x^{2}+6x+409 = 0$

Correct answer:

$2x^{2}+6x-391 = 0$

Explanation:

By the Pythagorean Theorem,

$x^{2}+ (x+3)^{2} = 20^{2}$

$x^{2}+ x^{2}+6x+9= 400$

$2x^{2}+6x-391 = 0$

Report an Error

Example Question #3 : How To Find The Length Of The Side Of A Right Triangle

Right_triangle

Note: Figure NOT drawn to scale.

Refer to the above diagram. Which of the following quadratic equations would yield the value of as a solution?

Possible Answers:

$x^{2} +4x+74= 0$

$x^{2} -4x-24= 0$

$x^{2} -4x+74= 0$

$2x^{2} -4x-24= 0$

$2x^{2} +4x-24= 0$

Correct answer:

$x^{2} -4x-24= 0$

Explanation:

By the Pythagorean Theorem,

$x^{2}+ (x+5)^{2} = (x+7)^{2}$

$x^{2}+ x^{2} +10x+25 = x^{2} +14x +49$

$2x^{2} +10x+25 = x^{2} +14x +49$

$x^{2} -4x-24= 0$

Report an Error

Example Question #4 : How To Find The Length Of The Side Of A Right Triangle

Right_triangle

Note: Figure NOT drawn to scale.

Refer to the above diagram.

AF = 6 , FD = 8

Find the length of $\overline{BC}$ .

Possible Answers:

$33\frac{1}{3}$

$22\frac{2}{9}$

$16\frac{2}{3}$

Correct answer:

$22\frac{2}{9}$

Explanation:

First, find .

Since $\overline{DF }$ is an altitude of right $\Delta ADB$ to its hypotenuse,

$\frac{FB}{FD}= \frac{FD}{AF}$

$\frac{FB}{8}= \frac{8}{6}$

$FB= \frac{8}{6} \cdot 8 = 10 \frac{2}{3}$

$AB = AF + FB = 6 + 10 \frac{2}{3} = 16 \frac{2}{3}$

$\Delta AFD \sim \Delta ABC$ by the Angle-Angle Postulate, so

$\frac{BC}{FD} = \frac{AB}{AF}$

$\frac{BC}{8} = \frac{16 \frac{2}{3}}{6}$

$BC = 16 \frac{2}{3}\cdot 8 \div 6 = 22\frac{2}{9}$

Report an Error

Example Question #5 : How To Find The Length Of The Side Of A Right Triangle

Right_triangle

Note: Figure NOT drawn to scale.

Refer to the above diagram.

DE = 6, EC = 12

Find the length of $\overline{AB}$ .

Possible Answers:

$7\frac{1}{4}$

$7\frac{1}{2}$

$7\frac{3}{4}$

Correct answer:

$7\frac{1}{2}$

Explanation:

First, find .

Since $\overline{DE}$ is an altitude of $\Delta CDB$ from its right angle to its hypotenuse,

$\Delta DEC \sim \Delta BED$

$\frac{BE}{DE}= \frac{ED}{EC}$

$\frac{BE}{6}= \frac{6}{12}$

$BE= \frac{6}{12} \cdot 6 = 3$

CB =BE + EC = 3+ 12 = 15

$\Delta DEC \sim \Delta ABC$ by the Angle-Angle Postulate, so

$\frac{AB}{DE} = \frac{CB}{CE}$

$\frac{AB}{6} = \frac{15}{12}$

$AB= \frac{15}{12} \cdot 6$

$AB = 7\frac{1}{2}$

Report an Error

Example Question #8 : Triangles

Right_triangle

Note: Figure NOT drawn to scale.

Refer to the above diagram. Evaluate .

Possible Answers:

$30\frac{3}{4}$

$3\frac{3}{8}$

$15\frac{3}{8}$

$6\frac{3}{4}$

Correct answer:

$3\frac{3}{8}$

Explanation:

By the Pythagorean Theorem,

$x^{2}+ 15^{2} = (x+12)^{2}$

$x^{2}+ 225 = x^{2}+24x+144$

225 = 24x+144

24x= 81

$x= 3\frac{3}{8}$

Report an Error

Example Question #6 : How To Find The Length Of The Side Of A Right Triangle

A right triangle $\Delta ABC$ with hypotenuse $\overline{AC}$ is inscribed in $\odot O$ , a circle with radius 26. If AB = 20 , evaluate the length of $\overline{BC}$ .

Possible Answers:

Insufficient information is given to answer the question.

Correct answer:

Explanation:

The arcs intercepted by a right angle are both semicircles, so hypotenuse $\overline{AC}$ shares its endpoints with two semicircles. This makes $\overline{AC}$ a diameter of the circle, and $AC = 2r = 2 \cdot 26 = 52$ .

By the Pythagorean Theorem,

$BC = \sqrt{(AC)^{2} - (AB)^{2}} = \sqrt{52^{2} -20^{2}} = \sqrt{2,704-400} = \sqrt{2,304} = 48$

Report an Error

View Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

View Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

View Tutors

Jaleesa
Certified Tutor

Pomona College, Bachelors, Africana Studies.

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Chicago, Spanish Tutors in Boston, Computer Science Tutors in Washington DC, GRE Tutors in Denver, Math Tutors in San Francisco-Bay Area, Reading Tutors in Atlanta, Computer Science Tutors in Atlanta, French Tutors in Miami, Computer Science Tutors in San Francisco-Bay Area, English Tutors in Dallas Fort Worth

Popular Courses & Classes

SAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Los Angeles, Spanish Courses & Classes in Denver, SSAT Courses & Classes in Houston, GRE Courses & Classes in New York City, GRE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Los Angeles, SAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Atlanta, ISEE Courses & Classes in Denver

Popular Test Prep

SAT Test Prep in Los Angeles, SAT Test Prep in Philadelphia, GRE Test Prep in Los Angeles, ISEE Test Prep in Atlanta, GRE Test Prep in New York City, LSAT Test Prep in Los Angeles, MCAT Test Prep in Washington DC, SAT Test Prep in Washington DC, GRE Test Prep in San Diego, ACT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : Triangles

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #1 : Acute / Obtuse Isosceles Triangles

Example Question #2 : Acute / Obtuse Isosceles Triangles

Example Question #661 : Grade 7

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

Example Question #3 : How To Find The Length Of The Side Of A Right Triangle

Example Question #4 : How To Find The Length Of The Side Of A Right Triangle

Example Question #5 : How To Find The Length Of The Side Of A Right Triangle

Example Question #8 : Triangles

Example Question #6 : How To Find The Length Of The Side Of A Right Triangle

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: