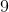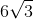PSAT Math : Diameter and Chords
Study concepts, example questions & explanations for PSAT Math
All PSAT Math Resources
Example Questions
Example Question #21 : Plane Geometry
The circle above has a radius of 
To solve a chord problem, draw right triangles using the chord, the radii, and a line connecting the center of the circle to the chord at a right angle.
Now, the chord is split into two equal pieces, and angle AOB is bisected. Instead of one 120 degree angle, you now have two 30-60-90 triangles. 30-60-90 triangles are characterized by having sides in the following ratio:
So, to find the length of the chord, first find the length of each half. Because the triangles in your circle are similar to the 30-60-90 triangle above, you can set up a proportion. The hypotenuse of our triangle is 6 (the radius of the circle) so it is set over 2 (the hypotenuse of our model 30-60-90 triangle). Half of the chord of the circle is the leg of the triangle that is across from the 60 degree angle (120/2), so it corresponds to the 
Therefore,
Because x is equal to half of the chord, the answer is 
Example Question #1 : How To Find The Ratio Of Diameter And Circumference
Let 
The formula for the area of a circle is 
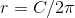
We can then substitute this value of r into the formula for the area:
Example Question #1 : Diameter And Chords
If the area of a circle is four times larger than the circumference of that same circle, what is the diameter of the circle?
32
4
16
2
8
16
Set the area of the circle equal to four times the circumference πr2 = 4(2πr).
Cross out both π symbols and one r on each side leaves you with r = 4(2) so r = 8 and therefore d = 16.
Example Question #302 : Circles
The perimeter of a circle is 36 π. What is the diameter of the circle?
3
36
6
72
18
36
The perimeter of a circle = 2 πr = πd
Therefore d = 36
Example Question #2 : Diameter And Chords
If the area of the circle touching the square in the picture above is 
Obtain the radius of the circle from the area.
Split the square up into 4 triangles by connecting opposite corners. These triangles will have a right angle at the center of the square, formed by two radii of the circle, and two 45-degree angles at the square's corners. Because you have a 45-45-90 triangle, you can calculate the sides of the triangles to be 
The area of the square is then 
Example Question #5 : Diameter
Two legs of a right triangle measure 3 and 4, respectively. What is the area of the circle that circumscribes the triangle?
For the circle to contain all 3 vertices, the hypotenuse must be the diameter of the circle. The hypotenuse, and therefore the diameter, is 5, since this must be a 3-4-5 right triangle.
The equation for the area of a circle is A = πr2.
Example Question #5 : How To Find The Length Of The Diameter
Note: Figure NOT drawn to scale.
In the above circle, the length of arc 
Call the diameter 
Example Question #1 : How To Find The Length Of The Diameter
Note: Figure NOT drawn to scale.
In the above circle, the length of arc 
Insufficient information exists to answer the question.
Call the diameter 
Certified Tutor
All PSAT Math Resources
