We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : How to find an angle in a rhombus

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #281 : Plane Geometry

In Rhombus 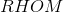RHOM $\displaystyle RHOM$, $m \angle H = 45 ^{\circ }$ $\displaystyle m \angle H = 45 ^{\circ }$. If $\overline{RO }$ $\displaystyle \overline{RO }$ is constructed, which of the following is true about $\Delta RHO$ $\displaystyle \Delta RHO$?

Possible Answers:

$\Delta RHO$ $\displaystyle \Delta RHO$ is right and isosceles, but not equilateral

$\Delta RHO$ $\displaystyle \Delta RHO$ is acute and equilateral

$\Delta RHO$ $\displaystyle \Delta RHO$ is right and scalene

$\Delta RHO$ $\displaystyle \Delta RHO$ is acute and scalene

$\Delta RHO$ $\displaystyle \Delta RHO$ is acute and isosceles, but not equilateral

Correct answer:

$\Delta RHO$ $\displaystyle \Delta RHO$ is acute and isosceles, but not equilateral

Explanation:

The figure referenced is below.

Rhombus

The sides of a rhombus are congruent by definition, so $\overline{RH} \cong \overline{HO}$ $\displaystyle \overline{RH} \cong \overline{HO}$, making $\Delta RHO$ $\displaystyle \Delta RHO$ isosceles. It is not equilateral, since $m \angle H = 45 ^{\circ }$ $\displaystyle m \angle H = 45 ^{\circ }$, and an equilateral triangle must have three $60 ^{\circ}$ $\displaystyle 60 ^{\circ}$ angles.

Also, consecutive angles of a rhombus are supplementary - as they are with all parallelograms - so

$m \angle HRM = 180^{\circ} - m \angle H = 180^{\circ} - 45 ^{\circ} = 135^{\circ}$ $\displaystyle m \angle HRM = 180^{\circ} - m \angle H = 180^{\circ} - 45 ^{\circ} = 135^{\circ}$

A diagonal of a rhombus bisects its angles, so

$m \angle HRO = \frac{1}{2} m \angle HRM = \frac{1}{2} \cdot 135 ^{\circ } = 67\frac{1}{2}^{\circ }$ $\displaystyle m \angle HRO = \frac{1}{2} m \angle HRM = \frac{1}{2} \cdot 135 ^{\circ } = 67\frac{1}{2}^{\circ }$

Similarly, $m \angle HOR = 67\frac{1}{2}^{\circ }$ $\displaystyle m \angle HOR = 67\frac{1}{2}^{\circ }$

This makes $\Delta RHO$ $\displaystyle \Delta RHO$ acute.

The correct response is that $\Delta RHO$ $\displaystyle \Delta RHO$ is acute and isosceles, but not equilateral.

Report an Error

View PSAT Mathematics Tutors

Gary
Certified Tutor

SUNY at Albany, Bachelor of Science, Economics. Pace University-New York, Masters in Business Administration, Analysis and Fu...

View PSAT Mathematics Tutors

Shakeel
Certified Tutor

View PSAT Mathematics Tutors

Connor
Certified Tutor

Grand Valley State University, Bachelors, Math and Statistics.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Boston, MCAT Tutors in Miami, GRE Tutors in Los Angeles, ISEE Tutors in Philadelphia, Statistics Tutors in Atlanta, Statistics Tutors in San Francisco-Bay Area, Computer Science Tutors in Washington DC, Chemistry Tutors in Dallas Fort Worth, Algebra Tutors in Chicago, Spanish Tutors in Philadelphia

Popular Courses & Classes

ISEE Courses & Classes in Chicago, ACT Courses & Classes in Phoenix, SSAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Los Angeles, LSAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Houston, GRE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Phoenix, GRE Courses & Classes in New York City, SSAT Courses & Classes in Phoenix

Popular Test Prep

ISEE Test Prep in New York City, LSAT Test Prep in Los Angeles, GRE Test Prep in Dallas Fort Worth, ACT Test Prep in Phoenix, LSAT Test Prep in Washington DC, SAT Test Prep in Philadelphia, GRE Test Prep in Los Angeles, GMAT Test Prep in Miami, GRE Test Prep in San Diego, GMAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : How to find an angle in a rhombus

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #281 : Plane Geometry

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: