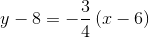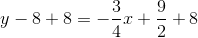All SAT II Math II Resources
Example Questions
Example Question #71 : Functions And Graphs
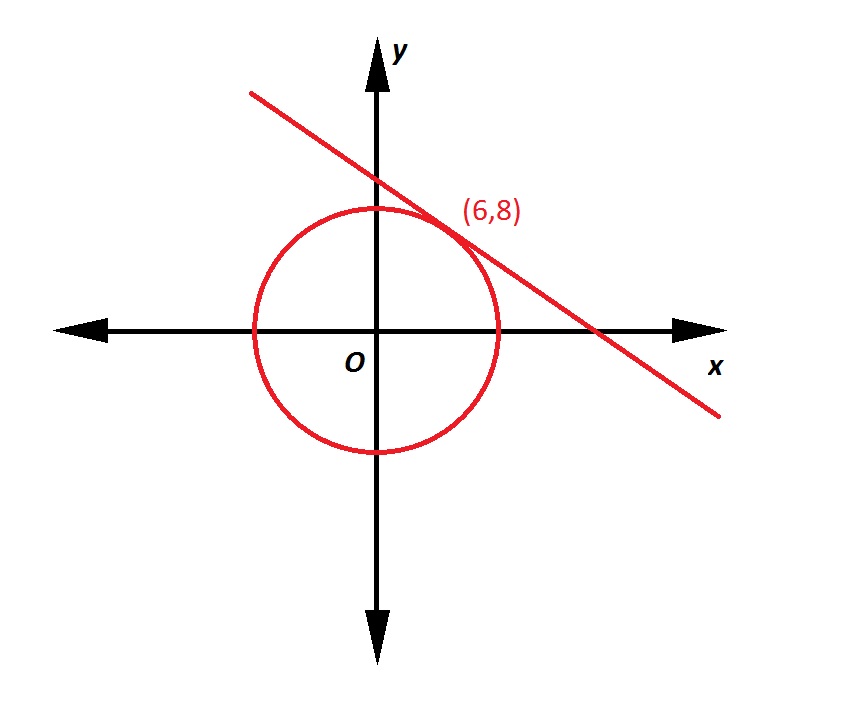
Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?
Possible Answers:
Insufficient information is given to determine the equation of the line.
Correct answer:
Explanation:
A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints 
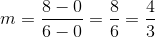
The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be 

Shivansh
Certified Tutor
Certified Tutor
University of British Columbia, Bachelor, Math major and data science minor .
All SAT II Math II Resources
Popular Subjects
Algebra Tutors in Seattle, Algebra Tutors in New York City, ACT Tutors in Houston, Statistics Tutors in San Diego, Calculus Tutors in Houston, Reading Tutors in Seattle, MCAT Tutors in Boston, Chemistry Tutors in New York City, Algebra Tutors in Dallas Fort Worth, GMAT Tutors in Philadelphia
Popular Courses & Classes
SSAT Courses & Classes in Atlanta, ACT Courses & Classes in Seattle, Spanish Courses & Classes in Denver, GMAT Courses & Classes in Chicago, GRE Courses & Classes in Los Angeles, LSAT Courses & Classes in San Diego, Spanish Courses & Classes in Philadelphia, SSAT Courses & Classes in Boston, MCAT Courses & Classes in Chicago, ISEE Courses & Classes in Houston
Popular Test Prep
GMAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Houston, ACT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Boston, GRE Test Prep in San Diego, ISEE Test Prep in Miami, GMAT Test Prep in Chicago, SSAT Test Prep in Washington DC, LSAT Test Prep in Los Angeles, ISEE Test Prep in Boston