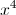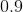All SAT Math Resources
Example Questions
Example Question #41 : Basic Squaring / Square Roots
If all real values of 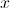
If 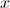

Example Question #42 : Basic Squaring / Square Roots
Evaluate:
0.082
0.0064
0.00064
0.00064
0.64
0.064
0.0064
0.08 * 0.08
First square 8:
8 * 8 = 64
Then move the decimal four places to the left:
0.0064
Example Question #1 : How To Find The Square Root Of A Decimal
Find the square root of the following decimal:
The easiest way to find the square root of a fraction is to convert it into scientific notation.
The key is that the exponent in scientific notation has to be even for a square root because the square root of an exponent is diving it by two. The square root of 9 is 3, so the square root of 8.1 is a little bit less than 3, around 2.8
Example Question #1 : How To Find The Square Root Of A Decimal
Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.
Because 
Example Question #2 : Basic Squaring / Square Roots
Find the square root of the following decimal:
This problem can be solve more easily by rewriting the decimal into scientific notation.
Because 
Example Question #381 : Arithmetic
Find the square root of the following decimal:
This problem becomes much simpler if we rewrite the decimal in scientific notation
Because 
Example Question #1 : How To Find The Square Root Of A Decimal
Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.
Because 
Example Question #22 : Decimals
Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.
Because 


Example Question #1 : How To Find The Square Root Of A Decimal
Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.
Because 
Example Question #2 : How To Find The Square Root Of A Decimal
Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.
Because 
Certified Tutor
All SAT Math Resources