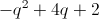SAT Mathematics : Simplifying Polynomials
Study concepts, example questions & explanations for SAT Mathematics
All SAT Mathematics Resources
Example Questions
Example Question #1 : Simplifying Polynomials
Choose the answer which best simplifies the following expression:
To solve this problem simply remove the parentheses and add the like terms:
Example Question #2 : Simplifying Polynomials
Choose the answer which best simplifies the following expression:
To solve this problem simply remove the parentheses and add the like terms:
Example Question #3 : Simplifying Polynomials
Choose the answer which best simplifies the following expression:
To simplify, simply remove the parentheses and combine like terms:
Example Question #4 : Simplifying Polynomials
Choose the answer that best simplifies the following expression:
To simplify, remove parentheses and combine like terms:
Example Question #5 : Simplifying Polynomials
Choose the answer that best simplifies the following expression:
To simplify, remove parentheses and combine like terms, but make sure to distribute the negative across all terms in the second set of parentheses, changing the sign of each:
Then combine like terms:
Example Question #6 : Simplifying Polynomials
Choose the answer that best simplifies the following expression:
To simplify, remove parentheses and combine like terms, remembering the ever-important step of applying the negative sign to each term within the second set of parentheses:
Example Question #7 : Simplifying Polynomials
Choose the answer that best simplifies the following expression:
To simplify, remove parentheses and combine like terms, remembering to distribute the negative (by changing each sign) for the terms in the second set of parentheses:
Example Question #36 : Polynomials & Quadratics
Simplify the following expression:
This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.
Add like terms together:
Combine these terms into one expression to find the answer:
Example Question #8 : Simplifying Polynomials
Simplify the following expression:
To simplify this expression you need to carefully remove the parentheses by distributing the negative sign across all terms in the second set of parentheses. To do this, just take the opposite of each of those signs. That gives you:
Then you can combine like terms:
Example Question #38 : Polynomials & Quadratics
Choose the answer that best simplifies the following expression:
To solve this expression, you need to remove the parentheses, being careful to account for the negative prior to the second set of parentheses. To distribute that negative, take the opposite of each sign for that set of values. Then, combine like terms:
All SAT Mathematics Resources
