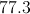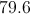Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : Mean

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #81 : Statistics & Probability

In a group of 4 books, the average number of pages is is 10. Juan adds a book with 20 pages to the group. What is the new average number of pages?

Possible Answers:

$\displaystyle 30$

$\displaystyle 20$

$\displaystyle 12$

$\displaystyle 15$

$\displaystyle 10$

Correct answer:

$\displaystyle 12$

Explanation:

If the average of 4 books was 10, then the total number of pages was $4\times10 =40$ $\displaystyle 4\times10 =40$ . Adding in the 20 new pages, but now dividing by 5 you get $\displaystyle 60/5 = 12$ .

Report an Error

Example Question #1 : Mean

Give the mean of the data set (nearest tenth, if applicable):

$\left \{ 56,78,98,85,77,73 \right \}$ $\displaystyle \left \{ 56,78,98,85,77,73 \right \}$

Possible Answers:

77.8 $\displaystyle 77.8$

75.7 $\displaystyle 75.7$

76.5 $\displaystyle 76.5$

77.3 $\displaystyle 77.3$

79.6 $\displaystyle 79.6$

Correct answer:

77.8 $\displaystyle 77.8$

Explanation:

Add the six elements and divide the sum by 6:

$\displaystyle 56 + 78 + 98 + 85 +77 + 73 = 467$

$467 \div 6 \approx 77.8$ $\displaystyle 467 \div 6 \approx 77.8$

Report an Error

Example Question #82 : Statistics & Probability

Find the mean of this set of numbers:

54, 41, 99, 120, 66.

Possible Answers:

$\displaystyle 80$

$\displaystyle 79$

$\displaystyle 99$

$\displaystyle 76$

Correct answer:

$\displaystyle 76$

Explanation:

Firrst, add the numbers:

$\displaystyle 54+41+99+120+66=380$

Then, divide by the amount of numbers in the set:

$380\div 5=76$ $\displaystyle 380\div 5=76$

Answer: The mean is 76.

Report an Error

Example Question #1 : Mean

Give the mean of the following eight scores:

$\left \{ 61, 67, 80, 72, 76, 73, 90, 68 \right \}$ $\displaystyle \left \{ 61, 67, 80, 72, 76, 73, 90, 68 \right \}$

Possible Answers:

72.5 $\displaystyle 72.5$

72.875 $\displaystyle 72.875$

73.375 $\displaystyle 73.375$

75.5 $\displaystyle 75.5$

$\displaystyle 73$

Correct answer:

73.375 $\displaystyle 73.375$

Explanation:

Divide the sum of the scores by eight:

$\frac{ 61+ 67+80+72+76+73+90+ 68}{8} = \frac{ 587}{8} = 73.375$ $\displaystyle \frac{ 61+ 67+80+72+76+73+90+ 68}{8} = \frac{ 587}{8} = 73.375$

Report an Error

Example Question #1 : Mean

Give the mean of the following nine scores:

$\left \{ 61, 67, 80, 72, 76, 73, 90, 68, 70 \right \}$ $\displaystyle \left \{ 61, 67, 80, 72, 76, 73, 90, 68, 70 \right \}$

Possible Answers:

75.5 $\displaystyle 75.5$

$\displaystyle 72$

$\displaystyle 68$

72.5 $\displaystyle 72.5$

$\displaystyle 73$

Correct answer:

$\displaystyle 73$

Explanation:

Divide the sum of the scores by nine:

$\frac{ 61 + 67+ 80+ 72+ 76+73+90+68+70}{9} = \frac{ 657}{9} = 73$ $\displaystyle \frac{ 61 + 67+ 80+ 72+ 76+73+90+68+70}{9} = \frac{ 657}{9} = 73$

Report an Error

Example Question #1 : Find Median

Give the median of the following eight scores:

$\left \{ 61, 67, 80, 72, 76, 73, 90, 68 \right \}$ $\displaystyle \left \{ 61, 67, 80, 72, 76, 73, 90, 68 \right \}$

Possible Answers:

72.5 $\displaystyle 72.5$

$\displaystyle 72$

73.375 $\displaystyle 73.375$

75.5 $\displaystyle 75.5$

$\displaystyle 73$

Correct answer:

72.5 $\displaystyle 72.5$

Explanation:

Arrange the scores from least to greatest.

$\left \{ 61, 67, 68, 72, 73, 76, 80, 90 \right \}$ $\displaystyle \left \{ 61, 67, 68, 72, 73, 76, 80, 90 \right \}$

There are an even number (eight) of scores, so the median is the arithmetic mean of the middle two scores, 72 and 73. This makes the median

$\frac{72 + 73}{2} = 72.5$ $\displaystyle \frac{72 + 73}{2} = 72.5$

Report an Error

Example Question #2 : Mean

The average age of 4 people is 12. What will be the sum of their ages in 3 years?

Possible Answers:

$\displaystyle 24$

$\displaystyle 15$

$\displaystyle 12$

$\displaystyle 60$

$\displaystyle 56$

Correct answer:

$\displaystyle 60$

Explanation:

The current sum of their ages is $12\times 4=48$ $\displaystyle 12\times 4=48$ . Since all 4 people will gain 3 years in age, we have to add 12 to the current sum.

Report an Error

Example Question #4 : How To Find Mean

What is the mean of the values $\displaystyle 34$ , $\displaystyle 40$ , $\displaystyle 1$ , $\displaystyle 9$ , 21? $\displaystyle 21?$

Possible Answers:

$\displaystyle 40$

$\displaystyle 5$

$\displaystyle 34$

$\displaystyle 21$

105 $\displaystyle 105$

Correct answer:

$\displaystyle 21$

Explanation:

The mean of a set of values can be calculated by adding the values together and dividing by the number of values: $\frac{34+40+1+9+21}{5}=21$ $\displaystyle \frac{34+40+1+9+21}{5}=21$

Report an Error

Example Question #1 : Mean

On the first four exams, Charley scored 92, 88, 76, and 74. Charley wants to have a test average of 85%. What must Charley score on the fifth exam to average 85%?

Possible Answers:

100%

82%

95%

90%

85%

Correct answer:

95%

Explanation:

The summation of the first four exams equals 330. Using the equation for average, Charley needs to get a 95 on the last exam.

$\frac{330+x}{5}=85$ $\displaystyle \frac{330+x}{5}=85$

$\displaystyle 330+x=85*5=425$

$\displaystyle x=425-330=95$

x=95 $\displaystyle x=95$

Report an Error

Example Question #4 : Find Measures Of Center, Variability, And Patterns In Data: Ccss.Math.Content.6.Sp.B.5c

Give the mean of the following data set:

$\left \{1, 2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 6, 6, 7, 9, 10 \right \}$ $\displaystyle \left \{1, 2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 6, 6, 7, 9, 10 \right \}$

Possible Answers:

5.375 $\displaystyle 5.375$

5.0625 $\displaystyle 5.0625$

$\displaystyle 6$

5.5 $\displaystyle 5.5$

$\displaystyle 5$

Correct answer:

5.0625 $\displaystyle 5.0625$

Explanation:

Since there are 16 elements, divide their sum by 16 to get the mean:

$(1+ 2+ 3+ 3+ 4+ 4+ 4+ 5+ 5+ 6+ 6+ 6+ 6+ 7+ 9+ 10) \div 16 = 81 \div 16 = 5.0625$ $\displaystyle (1+ 2+ 3+ 3+ 4+ 4+ 4+ 5+ 5+ 6+ 6+ 6+ 6+ 7+ 9+ 10) \div 16 = 81 \div 16 = 5.0625$

Report an Error

View SSAT- Middle Level Tutors

Lauren
Certified Tutor

Bryn Mawr College, Bachelors, History. University of Pittsburgh-Pittsburgh Campus, Masters, Library and Information Science.

View SSAT- Middle Level Tutors

Victorya
Certified Tutor

Amherst College, Bachelor of Science, American Studies. University of Massachusetts-Boston, Master of Science, Mathematics Te...

View SSAT- Middle Level Tutors

Ingrid
Certified Tutor

Northern Illinois University, Bachelor of Science, Elementary Education. Northern Illinois University, Master of Science, Cur...

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in San Diego, Biology Tutors in Washington DC, Computer Science Tutors in Los Angeles, Algebra Tutors in New York City, SSAT Tutors in Los Angeles, ACT Tutors in Miami, Reading Tutors in Houston, English Tutors in Washington DC, Biology Tutors in San Francisco-Bay Area, ACT Tutors in Boston

Popular Courses & Classes

GMAT Courses & Classes in Houston, MCAT Courses & Classes in Miami, GRE Courses & Classes in Seattle, SAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Miami, SAT Courses & Classes in Atlanta, SSAT Courses & Classes in Atlanta, GMAT Courses & Classes in New York City, Spanish Courses & Classes in New York City, MCAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SSAT Test Prep in Houston, SAT Test Prep in Seattle, ISEE Test Prep in Boston, MCAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Atlanta, SAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Washington DC, GRE Test Prep in Miami, SSAT Test Prep in Chicago, GRE Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Mean

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #81 : Statistics & Probability

Example Question #1 : Mean

Example Question #82 : Statistics & Probability

Example Question #1 : Mean

Example Question #1 : Mean

Example Question #1 : Find Median

Example Question #2 : Mean

Example Question #4 : How To Find Mean

Example Question #1 : Mean

Example Question #4 : Find Measures Of Center, Variability, And Patterns In Data: Ccss.Math.Content.6.Sp.B.5c

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: