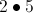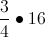We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : How to find the decimal equivalent of a fraction

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Decimal Equivalent Of A Fraction

Write the decimal equivalent of $\frac{3}{400}$ $\displaystyle \frac{3}{400}$.

Possible Answers:

0.006 $\displaystyle 0.006$

0.00675 $\displaystyle 0.00675$

0.009 $\displaystyle 0.009$

0.00625 $\displaystyle 0.00625$

0.0075 $\displaystyle 0.0075$

Correct answer:

0.0075 $\displaystyle 0.0075$

Explanation:

$\frac{3}{400} = 3 \div 400 = 0.0075$ $\displaystyle \frac{3}{400} = 3 \div 400 = 0.0075$

Report an Error

Example Question #2 : How To Find The Decimal Equivalent Of A Fraction

Express 0.014 as a fraction in lowest terms.

Possible Answers:

$\frac{7}{50}$ $\displaystyle \frac{7}{50}$

$\frac{7}{200}$ $\displaystyle \frac{7}{200}$

$\frac{7}{2,000}$ $\displaystyle \frac{7}{2,000}$

$\frac{7}{500}$ $\displaystyle \frac{7}{500}$

$\frac{14}{1,000}$ $\displaystyle \frac{14}{1,000}$

Correct answer:

$\frac{7}{500}$ $\displaystyle \frac{7}{500}$

Explanation:

The fraction has its last nonzero digit in the thousandths place, so write the number, without the decimal point, over 1,000. Then reduce.

$\frac{14}{1,000} =\frac{14\div 2}{1,000\div 2} = \frac{7}{500}$ $\displaystyle \frac{14}{1,000} =\frac{14\div 2}{1,000\div 2} = \frac{7}{500}$

Report an Error

Example Question #3 : How To Find The Decimal Equivalent Of A Fraction

Express $\frac{3}{400}$ $\displaystyle \frac{3}{400}$ as a decimal.

Possible Answers:

0.00625 $\displaystyle 0.00625$

0.00675 $\displaystyle 0.00675$

0.006 $\displaystyle 0.006$

0.009 $\displaystyle 0.009$

0.0075 $\displaystyle 0.0075$

Correct answer:

0.0075 $\displaystyle 0.0075$

Explanation:

$\frac{3}{400} = 3 \div 400 = 0.0075$ $\displaystyle \frac{3}{400} = 3 \div 400 = 0.0075$

Report an Error

Example Question #4 : How To Find The Decimal Equivalent Of A Fraction

Which of the following is NOT equal to $0.5 \bullet 20$ $\displaystyle 0.5 \bullet 20$?

Possible Answers:

$\frac{1}{5} \bullet 50$ $\displaystyle \frac{1}{5} \bullet 50$

$\frac{3}{4} \bullet 16$ $\displaystyle \frac{3}{4} \bullet 16$

$2 \bullet 5$ $\displaystyle 2 \bullet 5$

$\frac{2}{3} \bullet 15$ $\displaystyle \frac{2}{3} \bullet 15$

$\frac{1}{4} \bullet 40$ $\displaystyle \frac{1}{4} \bullet 40$

Correct answer:

$\frac{3}{4} \bullet 16$ $\displaystyle \frac{3}{4} \bullet 16$

Explanation:

All of the answer choices multiply to give you 10 except

$\frac{3}{4} \bullet 16$ $\displaystyle \frac{3}{4} \bullet 16$

so that is the correct answer.

Report an Error

Example Question #5 : How To Find The Decimal Equivalent Of A Fraction

What fractions equals 0.5 $\displaystyle 0.5$?

Possible Answers:

$\frac{8}{32}$ $\displaystyle \frac{8}{32}$

$\frac{8}{4}$ $\displaystyle \frac{8}{4}$

$\frac{8}{2}$ $\displaystyle \frac{8}{2}$

$\frac{8}{16}$ $\displaystyle \frac{8}{16}$

$\frac{8}{12}$ $\displaystyle \frac{8}{12}$

Correct answer:

$\frac{8}{16}$ $\displaystyle \frac{8}{16}$

Explanation:

0.5 $\displaystyle 0.5$ is equal to $\frac{1}{2}$ $\displaystyle \frac{1}{2}$.

Thus we are looking for a fraction that reduces to $\frac{1}{2}$ $\displaystyle \frac{1}{2}$.

$\frac{8}{12}$ $\displaystyle \frac{8}{12}$ reduces to $\frac{2}{3}$ $\displaystyle \frac{2}{3}$ (divide numerator and denominator by 4).

$\frac{8}{4}$ $\displaystyle \frac{8}{4}$ reduces to 2 (divide numerator and denominator by 4).

$\frac{8}{2}$ $\displaystyle \frac{8}{2}$ reduces to 4 (divide numerator and denominator by 2).

$\frac{8}{32}$ $\displaystyle \frac{8}{32}$ reduces $\frac{1}{4}$ $\displaystyle \frac{1}{4}$ (divide numerator and denominator by 4).

$\frac{8}{16}$ $\displaystyle \frac{8}{16}$ is the only one that reduces to $\frac{1}{2}$ $\displaystyle \frac{1}{2}$ (divide numerator and denominator by 8).

Report an Error

Example Question #5 : How To Find The Decimal Equivalent Of A Fraction

Write as a decimal:

$\frac{5}{9}$ $\displaystyle \frac{5}{9}$

Possible Answers:

0.5 $\displaystyle 0.5$

$0.\overline{54}$ $\displaystyle 0.\overline{54}$

$0.\overline{45}$ $\displaystyle 0.\overline{45}$

$0.5\overline{4}$ $\displaystyle 0.5\overline{4}$

$0.\overline{5}$ $\displaystyle 0.\overline{5}$

Correct answer:

$0.\overline{5}$ $\displaystyle 0.\overline{5}$

Explanation:

$5 \div 9 = 0.5555...$ $\displaystyle 5 \div 9 = 0.5555...$

That is, the digit 5 will repeat infinitely. This can be written as $0.\overline{5}$ $\displaystyle 0.\overline{5}$.

Report an Error

Example Question #6 : How To Find The Decimal Equivalent Of A Fraction

Write as a decimal:

$\frac{9}{11}$ $\displaystyle \frac{9}{11}$

Possible Answers:

0.81 $\displaystyle 0.81$

$0.\overline{8}$ $\displaystyle 0.\overline{8}$

$0.\overline{81}$ $\displaystyle 0.\overline{81}$

$0.8\overline{1}$ $\displaystyle 0.8\overline{1}$

0.9 $\displaystyle 0.9$

Correct answer:

$0.\overline{81}$ $\displaystyle 0.\overline{81}$

Explanation:

$9 \div 11 = 0.81818181...$ $\displaystyle 9 \div 11 = 0.81818181...$

That is, the group "81" will repeat infinitely. This quotient can be written as $0.\overline{81}$ $\displaystyle 0.\overline{81}$.

Report an Error

Example Question #7 : How To Find The Decimal Equivalent Of A Fraction

Rewrite as a decimal:

$\frac{7}{12}$ $\displaystyle \frac{7}{12}$

Possible Answers:

0.575 $\displaystyle 0.575$

$0.\overline{53}$ $\displaystyle 0.\overline{53}$

$0.58\overline{3}$ $\displaystyle 0.58\overline{3}$

$0.5\overline{3}$ $\displaystyle 0.5\overline{3}$

0.58 $\displaystyle 0.58$

Correct answer:

$0.58\overline{3}$ $\displaystyle 0.58\overline{3}$

Explanation:

$7 \div 12 = 0.583333...$ $\displaystyle 7 \div 12 = 0.583333...$

That is, after 5 and 8, the digit 3 will repeat infinitely. This can be rewritten as $0.58\overline{3}$ $\displaystyle 0.58\overline{3}$.

Report an Error

Example Question #8 : How To Find The Decimal Equivalent Of A Fraction

Write as a decimal:

$\frac{5}{18}$ $\displaystyle \frac{5}{18}$

Possible Answers:

$0.\overline{27}$ $\displaystyle 0.\overline{27}$

$0.\overline{277}$ $\displaystyle 0.\overline{277}$

0.2727 $\displaystyle 0.2727$

0.27 $\displaystyle 0.27$

$0.2\overline{7}$ $\displaystyle 0.2\overline{7}$

Correct answer:

$0.2\overline{7}$ $\displaystyle 0.2\overline{7}$

Explanation:

$5 \div 18 = 0.27777...$ $\displaystyle 5 \div 18 = 0.27777...$

That is, after the 2, the digit 7 repeats infinitely. This can be rewritten as $0.2\overline{7}$ $\displaystyle 0.2\overline{7}$.

Report an Error

Example Question #9 : How To Find The Decimal Equivalent Of A Fraction

Express $\frac{9}{20}$ $\displaystyle \frac{9}{20}$ as a decimal.

Possible Answers:

0.33 $\displaystyle 0.33$

0.35 $\displaystyle 0.35$

0.45 $\displaystyle 0.45$

0.27 $\displaystyle 0.27$

0.36 $\displaystyle 0.36$

Correct answer:

0.45 $\displaystyle 0.45$

Explanation:

Divide the numerator by the denominator:

$9 \div 20 = 0.45$ $\displaystyle 9 \div 20 = 0.45$

Report an Error

View SSAT- Middle Level Tutors

Linda
Certified Tutor

Long Island University-C W Post Campus, Bachelors, Art Education.

View SSAT- Middle Level Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SSAT- Middle Level Tutors

Aneeb
Certified Tutor

CUNY Lehman College, Bachelor in Arts, Arts, General.

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Denver, SSAT Tutors in Houston, SAT Tutors in Chicago, Reading Tutors in New York City, Algebra Tutors in Dallas Fort Worth, GMAT Tutors in Denver, GRE Tutors in Denver, SSAT Tutors in Dallas Fort Worth, Math Tutors in Phoenix, Spanish Tutors in Philadelphia

Popular Courses & Classes

ACT Courses & Classes in San Diego, LSAT Courses & Classes in San Diego, MCAT Courses & Classes in New York City, LSAT Courses & Classes in Miami, Spanish Courses & Classes in Boston, ACT Courses & Classes in Denver, SSAT Courses & Classes in New York City, SSAT Courses & Classes in Washington DC, MCAT Courses & Classes in Washington DC, MCAT Courses & Classes in San Diego

Popular Test Prep

LSAT Test Prep in San Diego, GRE Test Prep in Washington DC, SAT Test Prep in Dallas Fort Worth, ACT Test Prep in San Diego, SSAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Boston, MCAT Test Prep in Phoenix, GMAT Test Prep in Seattle, ACT Test Prep in Denver, MCAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : How to find the decimal equivalent of a fraction

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #1 : How To Find The Decimal Equivalent Of A Fraction

Example Question #2 : How To Find The Decimal Equivalent Of A Fraction

Example Question #3 : How To Find The Decimal Equivalent Of A Fraction

Example Question #4 : How To Find The Decimal Equivalent Of A Fraction

Example Question #5 : How To Find The Decimal Equivalent Of A Fraction

Example Question #5 : How To Find The Decimal Equivalent Of A Fraction

Example Question #6 : How To Find The Decimal Equivalent Of A Fraction

Example Question #7 : How To Find The Decimal Equivalent Of A Fraction

Example Question #8 : How To Find The Decimal Equivalent Of A Fraction

Example Question #9 : How To Find The Decimal Equivalent Of A Fraction

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: