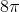The figure is a sector of a circle with radius 8; the sector has degree measure $\displaystyle 180 ^{\circ } - 45 ^{\circ }= 135 ^{\circ }$. The area of the sector is 

$\displaystyle A = \frac{ 135^{\circ }}{360 ^{\circ }} \cdot \pi r^{2}$

$\displaystyle A = \frac{ 135^{\circ }}{360 ^{\circ }} \cdot \pi \cdot 8^{2}$

$\displaystyle A = \frac{ 3}{8} \cdot 64 \pi$

$\displaystyle A = 24 \pi$

The figure is a semicircle - one-half of a circle - with radius 5.5, or $\displaystyle \frac{11}{2}$. Its area is one-half of the square of the radius multiplied by $\displaystyle \pi$ - that is, 

$\displaystyle A = \frac{1}{2} \pi r^{2}$

$\displaystyle A = \frac{1}{2} \pi \left (\frac{11}{2} \right )^{2}$

$\displaystyle A = \frac{1}{2} \pi \cdot \frac{121}{4}$

$\displaystyle A = \frac{121\pi}{8 }$

The equation of a circle on the coordinate plane is 

$\displaystyle x^{2} + y^{2} = r^{2}$,

where $\displaystyle r$ is the radius. Therefore, in this equation, 

$\displaystyle r^{2} = 66$.

The area of a circle is found using the formula

$\displaystyle A = \pi r^{2}$,

so we substitute 66 for $\displaystyle r^{2}$, yielding

$\displaystyle A = 66 \pi$.

If a right triangle is inscribed inside a circle, then the arc intercepted by the right angle is a semicircle, making the hypotenuse of triangle a diameter. 

The length of a hypotenuse of a 30-60-90 triangle is twice that of its short leg, so the hypotenuse of this triangle will be twice 11, or 22. The diameter of the circle is therefore 22, and the radius is half this, or 11. The area of the circle is therefore

$\displaystyle A = \pi r^{2} = \pi \cdot 11 ^{2} = 121 \pi$

Examine the following diagram:

If a (perpendicular) radius of the inscribed circle is constructed to the triangle, and a radius of the circumscribed circle is constructed to a neighboring vertex, a right triangle is formed. By symmetry, it can be shown that this is a 30-60-90 triangle, and, subsequently,

$\displaystyle BO = 2 \cdot AO$

If we let $\displaystyle r = AO$, the area of the inscribed circle is $\displaystyle A = \pi r^{2}$.

Then $\displaystyle BO = 2r$, and the area of the circumscribed circle is  $\displaystyle \pi\left ( 2r \right )^{2} = \pi \cdot 4r^{2} = 4 \pi r^{2} = 4A$

The ratio of the areas is therefore 4 to 1.

An equilateral triangle of perimeter 54 has sidelength one-third of this, or 18. 

Construct this triangle and its circumscribed circle, as well as a perpendicular bisector to one side and a radius to one of that side's endpoints:

Each side of the triangle has measure 18, so $\displaystyle AB = 9$. Also, the triangle formed by the segments, by symmetry, is a 30-60-90 triangle. By the 30-60-90 Theorem, 

$\displaystyle BO = \frac{AB}{\sqrt{3}} = \frac{9}{\sqrt{3}} = \frac{9\cdot \sqrt{3}}{\sqrt{3}\cdot \sqrt{3}} = \frac{9 \sqrt{3}}{3} = 3 \sqrt{3}$

and $\displaystyle AO = 2 \cdot BO = 2 \cdot 3\sqrt{3} = 6 \sqrt{3}$.

The latter is the radius, so the area of this circle is 

$\displaystyle A = \pi r^{2} = \pi (6 \sqrt{3})^{2} = \pi \cdot 6 ^{2} (\sqrt{3})^{2} = 36 \cdot 3 \cdot \pi = 108 \pi$

The figure below shows $\displaystyle \angle AOB$, which matches this description, along with its chord $\displaystyle \overline{AB}$:

By way of the Isosceles Triangle Theorem, $\displaystyle \Delta AOB$ can be proved equilateral, so $\displaystyle AB = AO= 7$. This is the radius, so the area is

$\displaystyle A = \pi r^{2} = \pi \cdot 7^{2}= 49 \pi$

If a right triangle is inscribed inside a circle, then the arc intercepted by the right angle is a semicircle, making the hypotenuse of the triangle a diameter. 

By the 30-60-90 Theorem, the length of the shorter leg of a 30-60-90 triangle is that of the longer leg divided by $\displaystyle \sqrt{3}$, so the shorter leg will have length $\displaystyle \frac{11}{\sqrt{3}}$; the hypotenuse will have length twice this length, or 

$\displaystyle 2 \cdot \frac{11}{\sqrt{3}} = \frac{22}{\sqrt{3}}$.

The diameter of the circle is therefore $\displaystyle \frac{22}{\sqrt{3}}$; the radius is half this, or $\displaystyle \frac{11}{\sqrt{3}}$. The area of the circle is therefore

$\displaystyle A = \pi r^{2} = \pi \cdot \left ( \frac{11}{\sqrt{3}} \right ) ^{2} = \frac{121}{3}\cdot \pi = \frac{121 \pi}{3}$

The figure below shows $\displaystyle \angle AOB$, which matches this description, along with its chord $\displaystyle \overline{AB}$:

By way of the Isoscelese Triangle Theorem, $\displaystyle \Delta AOB$ can be proved a 45-45-90 triangle with hypotenuse 15. By the 45-45-90 Theorem, its legs, each a radius, have length that can be determined by dividing this by $\displaystyle \sqrt{2}$:

$\displaystyle A O = \frac{AB }{\sqrt{2}} = \frac{15}{\sqrt{2}}$

The area is therefore

$\displaystyle A = \pi r^{2} = \pi \cdot \left ( \frac{15}{\sqrt{2}} \right )^{2} = \pi \cdot \frac{225}{2} =\frac{225 \pi}{2}$

An equilateral triangle of perimeter 72 has sidelength one-third of this, or 24. 

Construct this triangle and its inscribed circle, as well as a radius to one side - which, by symmetry, is a perpendicular bisector - and a segment to one of that side's endpoints:

Each side of the triangle has measure 24, so $\displaystyle AB = 12$. Also, the triangle formed by the segments, by symmetry, is a 30-60-90 triangle. Therefore, 

$\displaystyle BO = \frac{AB}{\sqrt{3}} = \frac{12}{\sqrt{3}} = \frac{12\cdot \sqrt{3}}{\sqrt{3}\cdot \sqrt{3}} = \frac{12 \sqrt{3}}{3} =4\sqrt{3}$

which is the radius of the circle. The area of this circle is 

$\displaystyle A = \pi r^{2} = \pi (4 \sqrt{3})^{2} = \pi \cdot 4 ^{2} (\sqrt{3})^{2} = 16\cdot 3 \cdot \pi= 48\pi$