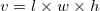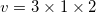All SSAT Upper Level Math Resources
Example Questions
Example Question #4 : Volume Of A Rectangular Solid
A given rectangular prism has a length of 


The volume of a given prism 



Substituting in our known values:
Example Question #52 : Volume Of A Three Dimensional Figure
Find the volume of a circular prism with a base radius of 

The volume of a given prism 



Substituting in our known values:
Example Question #53 : Volume Of A Three Dimensional Figure
A triangular prism has a triangle base length of 


Not enough information provided
The volume of a given prism 





Therefore, we can substitute the base area equation into the equation for the volume of a prism:
Substituting in our known values:
Example Question #252 : Geometry
A given rectangular prism has a length of 


The volume 



Example Question #1 : How To Find The Volume Of A Prism
A given rectangular prism has a length of 


The volume 



Example Question #901 : Ssat Upper Level Quantitative (Math)
What is the volume of the shape below?
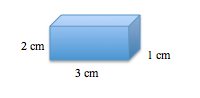
The formula for volume of a rectangular prism is
Remember, volume is always labeled as units to the third power.
Example Question #902 : Ssat Upper Level Quantitative (Math)
What is the volume of the shape below?

The formula for volume of a rectangular prism is
Remember, volume is always labeled as units to the third power.
Example Question #903 : Ssat Upper Level Quantitative (Math)
What is the volume of the shape below?

The formula for volume of a rectangular prism is
Remember, volume is always labeled as units to the third power.
Example Question #904 : Ssat Upper Level Quantitative (Math)
What is the volume of the shape below?

The formula for volume of a rectangular prism is
Remember, volume is always labeled as units to the third power.
Example Question #905 : Ssat Upper Level Quantitative (Math)
What is the volume of the shape below?

The formula for volume of a rectangular prism is
Remember, volume is always labeled as units to the third power.
Certified Tutor
Certified Tutor
All SSAT Upper Level Math Resources