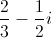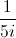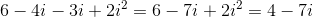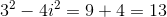Algebra II : Basic Operations with Complex Numbers
Study concepts, example questions & explanations for Algebra II
All Algebra II Resources
Example Questions
Example Question #1 : Basic Operations With Complex Numbers
What is the absolute value of
The absolute value is a measure of the distance of a point from the origin. Using the pythagorean distance formula to calculate this distance.
Example Question #1 : Basic Operations With Complex Numbers
Consider the following definitions of imaginary numbers:
Then,
Example Question #2 : Understanding Imaginary And Complex Numbers
Simplify the expression.
None of the other answer choices are correct.
Combine like terms. Treat 
Substitute to eliminate 
Simplify.
Example Question #1 : Basic Operations With Complex Numbers
What is the value of 
When dealing with imaginary numbers, we multiply by foiling as we do with binomials. When we do this we get the expression below:
Since we know that 
Example Question #1 : Basic Operations With Complex Numbers
What is the value of 
Recall that the definition of imaginary numbers gives that 
Example Question #1 : Basic Operations With Complex Numbers
Find 
Multiply the numerator and denominator by the numerator's complex conjugate.
Reduce/simplify.
Example Question #63 : Imaginary Numbers
Subtract:
This is essentially the following expression after translation:
Now add the real parts together for a sum of 
Example Question #7 : How To Add Integers
Multiply:
Answer must be in standard form.
The first step is to distribute which gives us:
which is in standard form.
Example Question #6 : How To Add Integers
Add:
When adding complex numbers, add the real parts and the imaginary parts separately to get another complex number in standard form.
Adding the real parts gives 
Example Question #2 : Complex Numbers
Divide:
The answer must be in standard form.
Multiply both the numerator and the denominator by the conjugate of the denominator which is 
The numerator after simplification give us
The denominator is equal to
Hence, the final answer in standard form =
All Algebra II Resources
